5  Metoda powierzchniowo-wagowa

• Granice jednostek spisowych zmieniają się między latami, co utrudnia wykonywanie analiz porównawczych. Przed przystąpieniem do analizy rasowo-etnicznej struktury ludności dla kilku lat, trzeba ujednolicić granice jednostek spisowych. Jedną z metod pozwalających na przekształcenie danych z jednego zestawu granic w inny jest metoda powierzchniowo-wagowa.

• Metoda powierzchniowo-wagowa (ang. areal interpolation, areal weightening interpolation) to rodzaj interpolacji powierzchniowej używanej do przekształcania danych geograficznych z jednego zestawu granic w inny. W metodzie tej wartości cechy (np. liczby ludności) przypisywane są do jednostki docelowej proporcjonalnie do odsetka powierzchni, w jakiej jednostka źródłowa pokrywa jednostkę docelową.

  • Jednostką źródłową (ang. source zone) jest pierwotny zestaw granic, w jakim zagregowana jest dana cecha.

  • Jednostką docelową (ang. target zone) jest wynikowy zestaw granic, do którego rozkładamy daną cechę (może nią być inny zestaw granic poligonowych lub siatka komórek rastra).

5.1 Przykład

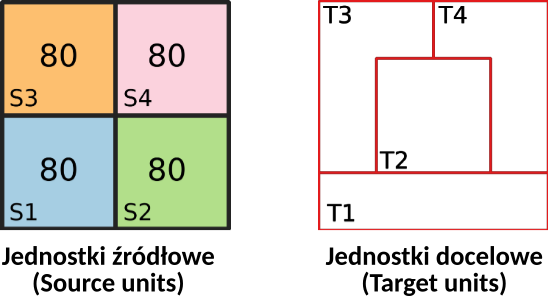
W roku X obszar został podzielony na 4 równe jednostki (S1-S4), każda zamieszkała przez 80 osób. W roku Y dla tego samego obszaru wprowadzono podział na 4 inne jednostki (T1-T4). Oblicz na podstawie danych z roku X, ile osób mieszka w jednostkach T1-T4?

Etap 1. Przecięcie granic jednostek źródłowych oraz jednostek docelowych

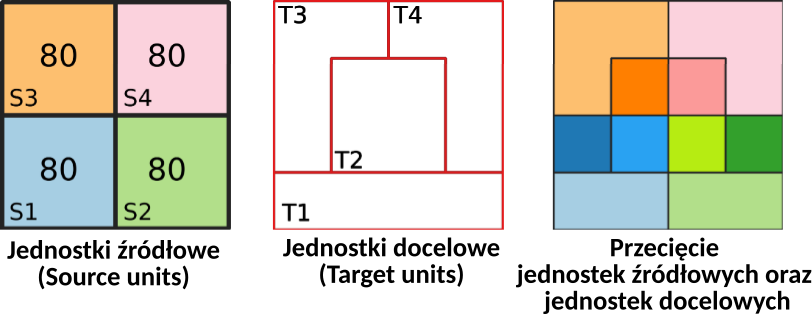
Etap 2. Obliczenie wagi dla każdej jednostki powstałej z przecięcia granic jednostek źródłowych oraz jednostek docelowych

W drugim etapie obliczane są wagi dla każdego poligonu powstałego z przecięcia granic jednostek źródłowych oraz jednostek docelowych. Wagi dla każdego przecięcia obliczane są według wzoru: \[W_i = \frac{A_i}{A_j}\]

gdzie

• \(W_i\) - waga “powierzchniowa” przypisana do każdego poligonu \(i\) powstałego z przecięcia granic źródłowych oraz docelowych;
• \(A_i\) - powierzchnia poligonu \(i\) powstałego z przecięcia granic źródłowych oraz docelowych;
• \(A_j\) - ogólna powierzchnia jednostki docelowej \(j\) do której należy poligon \(i\).

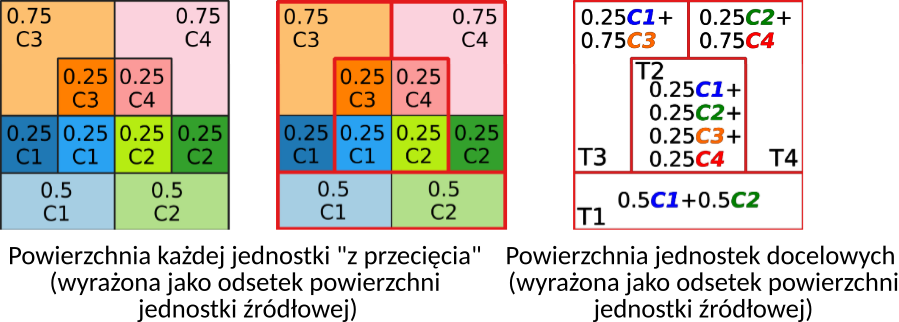
Etap 3. Przypisanie liczby ludności do każdej jednostki powstałej z przecięcia granic jednostek źródłowych oraz jednostek docelowych.

\[E_i = V_j \times W_i\] gdzie

• \(E_i\) - szacowana liczba osób dla każdego poligonu \(i\) powstałego z przecięcia;
• \(W_i\) - waga “powierzchniowa” przypisana do każdego poligonu \(i\) powstałego z przecięcia granic źródłowych oraz docelowych;
• \(V_j\) - liczba osób w jednostce źródłowej \(j\)

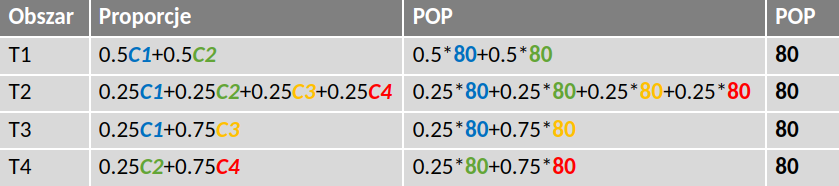
Etap 4. Zsumowanie liczby ludności z jednostek “z przecięcia” do granic jednostek docelowych

\[G_k = \sum E_{ik}\] gdzie

• \(G_k\) - suma wszystkich szacowanych wartości
• \(E_i\) - wchodzących w skład jednostki docelowej \(k\);
  
• \(E_{ik}\) - szacowane wartości ze wszystkich poligonów \(i\) wchodzących w skład jednostki docelowej \(k\)