18 Ćwiczenie 2

18.1 Cel ćwiczenia

Celem ćwiczeń jest stworzenie zestawu narzędzi (funkcji w języku R), które posłużą obliczeniu tradycyjnych miar segregacji oraz zróżnicowania rasowego. Funkcje/narzędzia będą wykorzystywane na kilku następych zajęciach.

Należy stworzyć narzędzia obliczające:

entropię \(E\) oraz entropię standaryzowaną \(E_{std}\)
wskaźnik teorii informacji \(H\)
wskaźnik niepodobieństwa \(D\)

Stworzone funkcje należy przetestować na kilku przykładach (dane testowe zostały zapisane w plikach przyklad_a.csv, przyklad_b.csv, przyklad_c.csv, przyklad_d.csv, dane_przykladowe.csv)

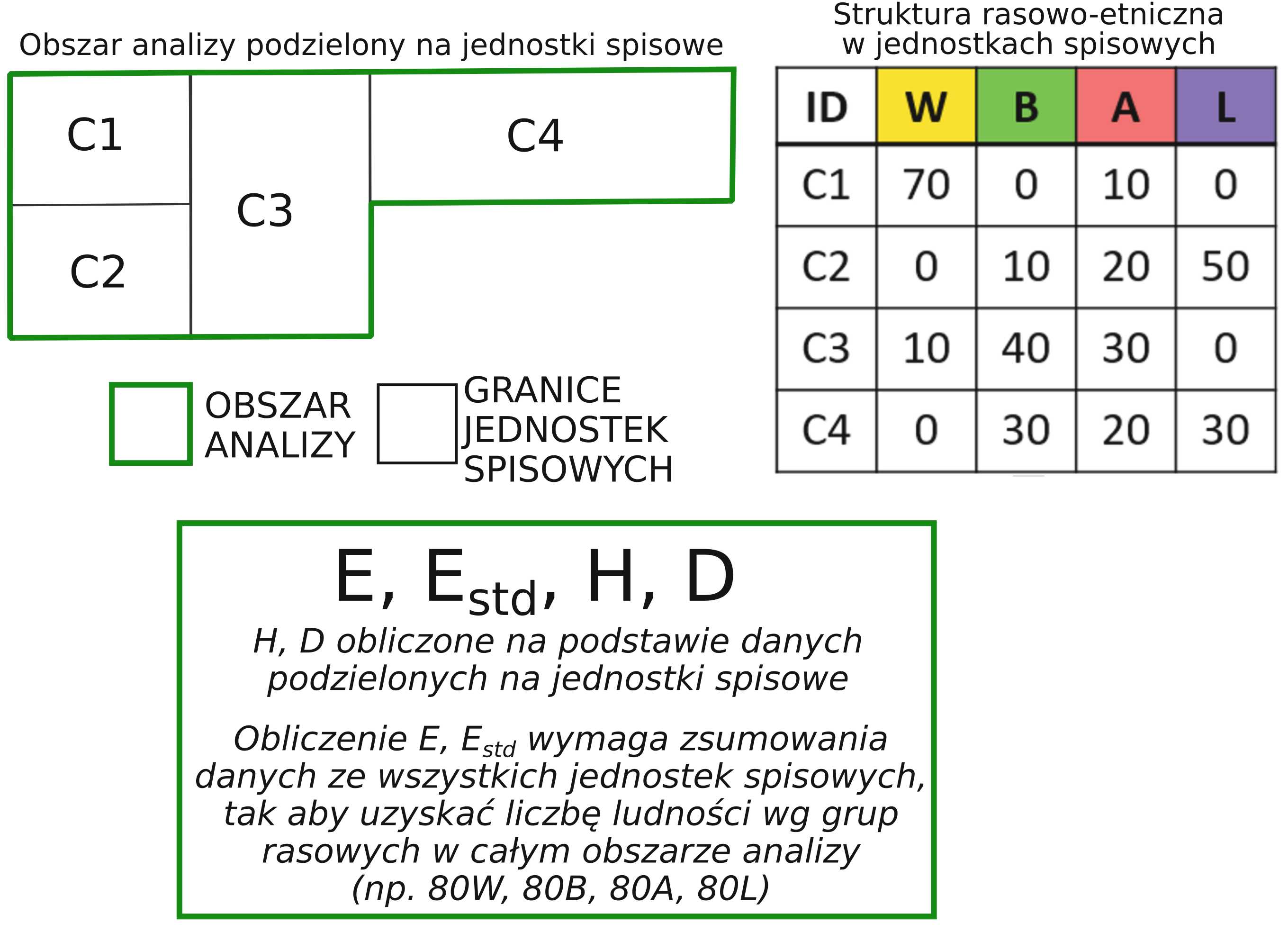
18.2 Zróżnicowanie oraz segregacja rasowa w analizowanym obszarze

Tradycyjne miary segregacji oraz zróżnicowania rasowo-etnicznego obliczane są na podstawie danych tabelarycznych przedstawiających liczbę osób wg kategorii rasowo-etnicznych w jednostkach spisowych, na które zostało podzielone miasto. Miary te obliczane są na poziomie hrabstw lub miast.
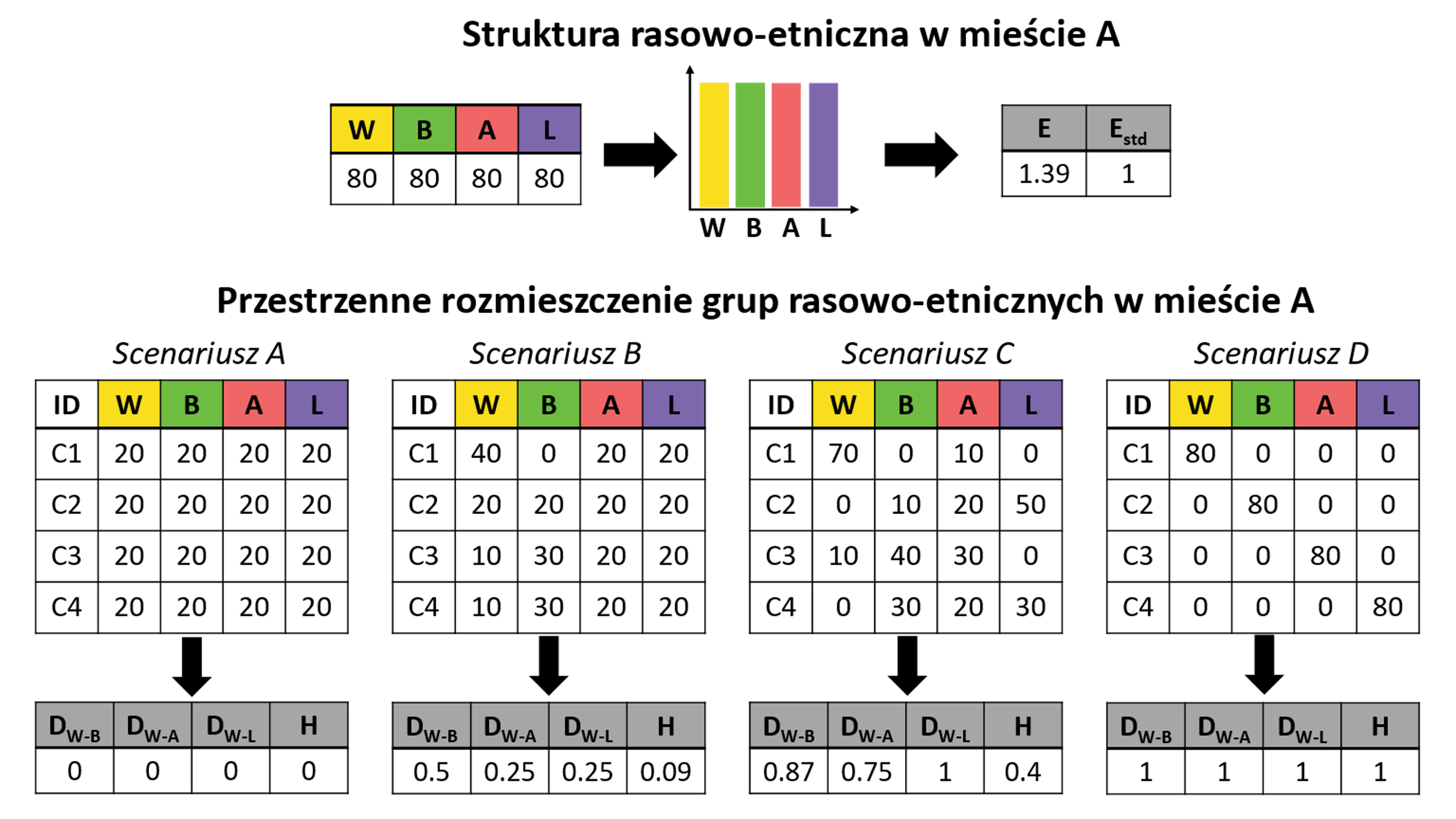
Obliczenie miar zróżnicowania rasowo-etnicznego wymaga zsumowania danych ze wszystkich jednostek spisowych, tak aby uzyskać liczbę ludności wg grup rasowo-etnicznych w całym obszarze analizy (np. 80W, 80B, 80A, 80L).
Obliczenie wskaźników segregacji rasowej wymaga podzielenia obszaru na mniejsze jednostki. Wartość wskaźnika zależy od przyjętego podziału na jednostki przestrzenne.

Rycina 1. Zróżnicowanie oraz segregacja rasowa w analizowanym obszarze (np. dla całego miasta)

18.3 Miary zróżnicowania rasowo-etnicznego

18.3.1 Entropia

Miarą zróżnicowania rasowego jest entropia obliczana według wzoru:

\[E = -\sum p_{k} \log p_{k}\] Obliczenia należy wykonać dla jednostek dla których liczba ludnosci jest większa od 0.

18.3.2 Entropia standaryzowana

Entropia standaryzowana obliczana jest według wzoru:

\[E_{std} = \frac{E}{E_{max}}\]

gdzie \(E\) - oznacza entropię, a \(E_{max}\) oznacza entropię maksymalną.

Entropia obliczana jest według wzoru: \[E = -\sum p_{k} \log p_{k}\]

Entropia maksymalna obliczana jest \(E_{max} = log(K)\), gdzie K to liczba grup rasowo-etnicznych.

18.4 Miary segregacji rasowo-etnicznej

18.4.1 Wskaźnik niepodobieństwa D

Wskaźnik niepodobieństwa D obliczany jest według wzoru:

\[D = \frac{1}{2}\sum_{i}^{N}\left\lvert \frac{a_{i}}{A} - \frac{b_{i}}{B} \right\rvert\]

\(a_{i}\) - liczba ludności grupy 1 w jednostce spisowej \(i\)
A - liczba ludności grupy 1 w analizowanym obszarze
\(b_{i}\) - liczba ludności grupy 2 w jednostce spisowej \(i\)
B - liczba ludności grupy 2 w analizowanym obszarze

18.4.2 Wskaźnik teorii informacji H.

Wskaźnik teorii informacji H obliczany jest według wzoru:

\[H = \sum_{i=1}^{N}\left [ \frac{t_{i}(E - E_{i})}{ET} \right ]\]

gdzie

\(E_{i}\) - entropia danej jednostki spisowej i,
\(E\) - entropia obliczona dla całego obszaru
\(t_{i}\) - liczba ludności danej jednostki spisowej i,
\(T\) - liczba ludności całego obszaru

18.5 Obliczanie miar zróżnicowania rasowego oraz segregacji rasowej w R.

18.5.1 Obliczanie entropii

Entropia \(E\) obliczana jest w następujący sposób:

Ćwiczenie 1

Oblicz entropię dla danych zawartych w plikach przyklad_a.csv, przyklad_b.csv, przyklad_c.csv, przyklad_d.csv, dane_przykladowe.csv

Ćwiczenie 2

Napisz funkcję w R obliczającą entropię.

Kilka uwag do obliczania entropii:

POP>0 - nie można dzielić przez 0
log(0) jest nieokreślony.

Przydatne rozwiązania - operacje na wektorach w R

a = c(0.125, 0.125, 0.25, 0.5)
a*2

[1] 0.25 0.25 0.50 1.00

log2(a)

[1] -3 -3 -2 -1

a*log2(a)

[1] -0.375 -0.375 -0.500 -0.500

-sum(a*log2(a))

[1] 1.75

18.6 Obliczanie entropii standaryzowanej

Ćwiczenie 1

Oblicz entropię standaryzowaną dla danych zawartych w plikach przyklad_a.csv, przyklad_b.csv, przyklad_c.csv, przyklad_d.csv, dane_przykladowe.csv

Ćwiczenie 2

Napisz funkcję w R obliczającą entropię standaryzowaną.

18.7 Obliczanie wskaźnika niepodobieństwa \(D\)

Dla 4 jednostek spisowych poniższy wzór na obliczenie wskaźnika niepodobieństwa będzie miał postać:

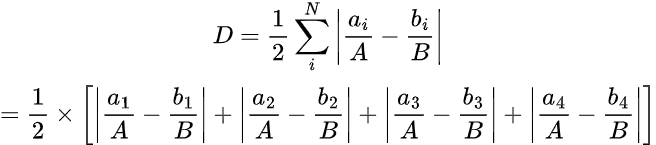
a, b to liczba osób danej grupy rasowej w jednostce spisowej, natomiast A i B to liczba osób z danej grupy rasowej zamieszkująca cały obszar.

Ćwiczenie 1

Oblicz wskaźnik niepodobieństwa między grupami W i B oraz W i L dla danych zawartych w pliku przyklad_b.csv

Ćwiczenie 2

Napisz funkcję w R obliczającą wskaźnik niepodobieństwa. Zastosuj tą funkcję do obliczenia wskaźników W-B, W-A, W-L dla danych zawartych w plikach przyklad_a.csv, przyklad_b.csv, przyklad_c.csv, przyklad_d.csv, dane_przykladowe.csv

18.8 Obliczanie wskaźnika wskaźnika teorii informacji H

Etapy obliczenia wskaźnika teorii informacji H

Obliczenie liczby osób mieszkających w każdej jednostce spisowej.
Obliczenie odsetka osób w każdej jednostce spisowej oraz w całym obszarze.
Obliczenie entropii dla każdej jednostki spisowej (\(E_{i}\))
Obliczenie wagi - odsetek ludności w jednostce spisowej w stosunku do liczby ludności całego obszaru (\(\frac{t_{i}}{T}\))
Obliczenie różnicy między entropią całego obszaru a entropią w jednostce spisowej (\(\frac{E - E_{i}}{E}\))
Pomnożenie wartości uzyskanych w punkcie (4) oraz (5)
Zsumowanie wartości uzyskanych w punkcie (6).

Ćwiczenie 1

Oblicz wskaźnik teorii informacji H dla danych zawartych w pliku przyklad_b.csv

Ćwiczenie 2

Napisz funkcję w R obliczającą wskaźnik teorii informacji H. Zastosuj tą funkcję do obliczenia wskaźników dla danych zawartych w plikach przyklad_a.csv, przyklad_b.csv, przyklad_c.csv, przyklad_d.csv, dane_przykladowe.csv

18.9 Wartości wskaźników dla wymienionych przykładów

Poniżej zostały zamieszczone wartości wskaźników segregacji oraz zróżnicowania rasowo-etnicznego dla w/w przykładów.

Przykłady A-D

Przykładowe dane

ID	BIALI	CZARNI	AZJACI	LATYNOSI	RDZENNI_AMERYKANIE	POZOSTALI	POP
40306	209	1450	130	2517	10	56	4372
40307	919	1431	915	1073	6	84	4428
40308	766	1374	278	1598	6	47	4069
40407	668	524	323	384	4	37	1940
40408	330	858	262	212	7	45	1714
40414	354	644	85	480	1	28	1592
40415	97	1376	44	899	8	42	2466
40416	576	977	278	709	4	65	2609

Wartości wskaźników dla przykładowych danych (przykladowe_dane.csv)

Dwa	Dwb	Dwl	H	E	Estd
0.1925452	0.2643989	0.3634019	0.0655884	1.347994	0.7523296