18  Analiza korelacji

18.1 Wprowadzenie

18.1.1 Podstawowe pojęcia

  • Analiza korelacji służy do “wychwycenia” czy zachodzi związek pomiędzy dwiema (lub więcej) zmiennymi.

  • Miarą korelacji jest współczynnik korelacji

  • Współczynnik korelacji dostarcza informacji o tym jaka jest siła związku (wartość współczynnika) oraz jaki jest kierunek związku (znak).

  • Dla każdego współczynnika korelacji należy także obliczyć jego istotność statystyczną, stosujac jeden z testów istotności przeznaczonych dla współczynników korelacji.

    • Hipoteza zerowa: ρ x,y=0
    • Hipoteza alternatywna: ρ x,y≠0 lub ρ x,y<0 lub ρ x,y>0

  • Zależność między zmiennymi może mieć charakter liniowy lub krzywoliniowy.

18.1.2 Korelacja a przyczynowość

  • Korelacja nie wskazuje na istnienie związku przyczynowo-skutkowego pomiędzy zmiennymi.

  • Innymi słowy: Istnienie korelacji liczbowej nie potwierdza, że jedno zjawisko powoduje drugie.

    • A może powodować B
    • B może powodować A
    • A lub B może być wywołane przez C
    • Zależność między A i B może być przypadkowa.

  • http://www.tylervigen.com/spurious-correlations

18.1.3 Kilka ważnych informacji

  • Najważniejsza jest isotność korelacji. Niepotrzebna nam korelacja nawet bardzo wysoka, jeśli nie jest istotna statystycznie.
  • Wartość współczynnika nawet bliska 0 nie zawsze oznacza brak zależności. Może oznaczać jedynie brak zależności liniowej.
  • Wielkość współczynnika podlega wpływom wartości skrajnych i odstających.

18.1.4 Korelacja liniowa

  • Miarą korelacji liniowej jest współczynnik korelacji Pearsona.

  • Współczynniki korelacji przyjmują wartości z przedziału od -1,00 do +1,00.

    • Wartość -1,00 - reprezentuje doskonałą korelację ujemną (współzależność pomiędzy zmiennymi kształtująca się w taki sposób, że gdy wartości jednej zmiennej wykazują tendencję rosnącą, wówczas wartości drugiej zmiennej wykazują tendencję malejącą)

    • wartość +1,00 - reprezentuje doskonałą korelacją dodatnią (współzależność pomiędzy zmiennymi przedstawia się w taki sposób, że gdy wartości jednej zmiennej wykazują tendencję wzrastającą, wówczas wartości drugiej zmiennej także wykazują tendencję wzrastającą).

    • Wartość 0.00 wyraża brak korelacji.

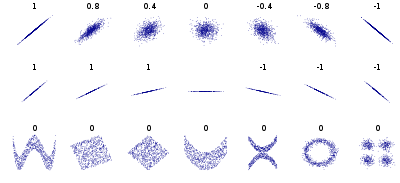
18.1.5 Jak silna jest korelacja?

Do opisu i interpretacji istotnej korelacji pomocne może być przyjęcie pewnej skali określającą siłę związku. Nie ma jednej przyjętej skali. Poniżej przedstawiam jedną z nich:

  • 0 - brak korelacji
  • 0,1 do 0,3 - słaba korelacja
  • 0,3 do 0,5 - przeciętna korelacja
  • 0,5 do 0,7 - korelacja wysoka
  • 0,7 do 0,9 - korelacja bardzo wysoka
  • 0,9 do 1 - korelacja prawie pełna

18.2 Demonstracja dla współczynnika korelacji liniowej

install.packages("TeachingDemos")
library("TeachingDemos")
put.points.demo(x = NULL, y = NULL, lsline = TRUE)

#Używając opcji Add Point dodaj punkty w oknie wykresu
#Zwróć uwagę jak zmienia się wartość współczynnika korelacji (r).

Zgadnij wartość współczynnika korelacji - https://gallery.shinyapps.io/correlation_game/

18.3 Testy korelacji

  • test korelacji liniowej Pearsona

    • stosowany gdy zmienne mają zależnośc liniową
    • zmienne mają rozkład normalny

  • test korelacji rang Spearman

    • stosowany gdy naruszone jest założenie o normalności rozkładu (np. gdy istnieją wartości odstające)

18.4 Korelacja liniowa

set.seed(25)
x = rnorm(1000)
y = x + rnorm(1000)
df = data.frame(x, y)
library(ggplot2)
ggplot(df, aes(x, y)) + geom_point() + stat_smooth(method = lm)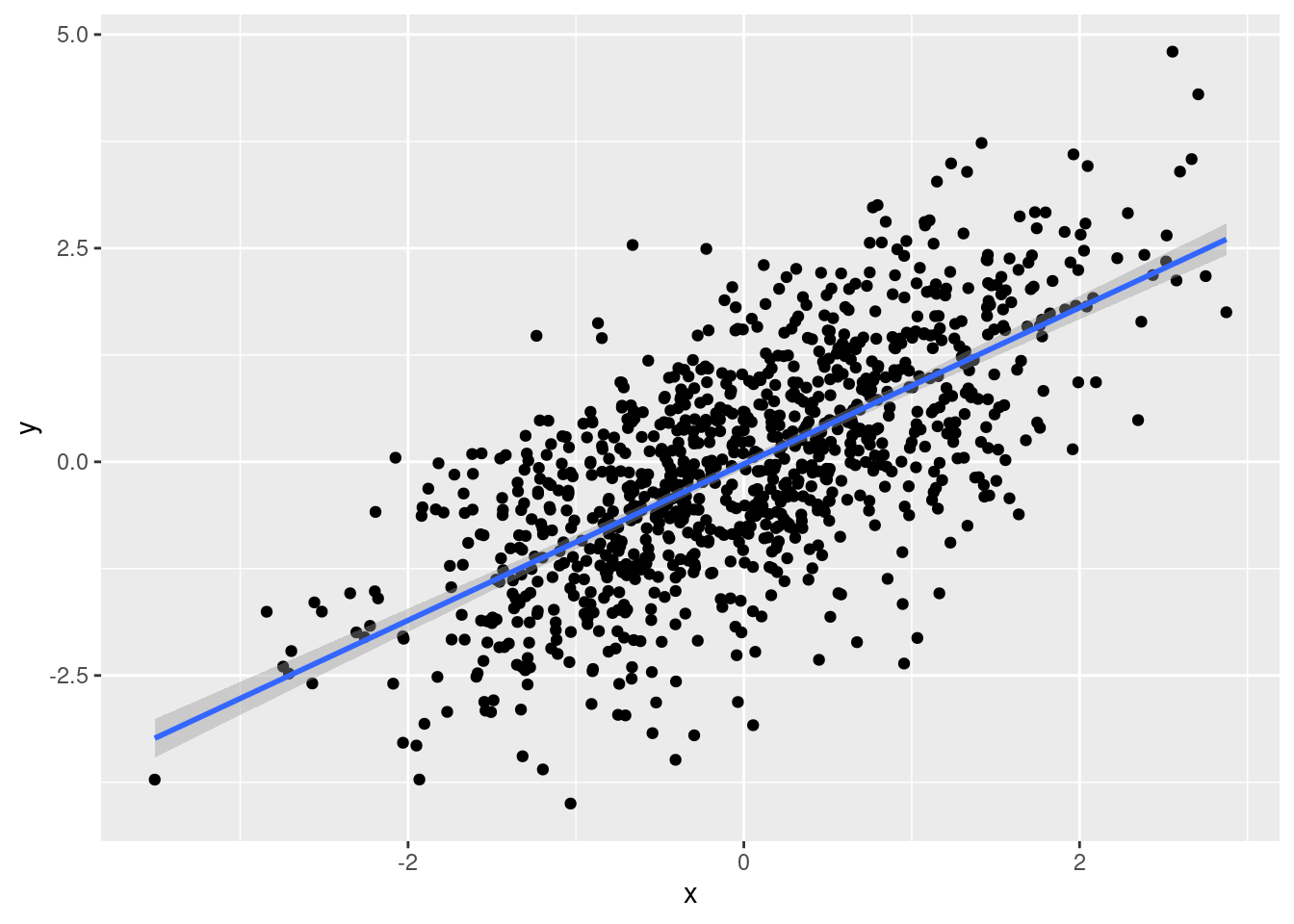

18.4.1 Zbadanie normalności rozkładu

ggplot(df) + 
  geom_histogram(aes(x = x), col = "darkblue", fill = "darkblue") + 
  geom_histogram(aes(x = y), col = "lightblue", fill = "lightblue", alpha = 0.7) + 
theme_bw()
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.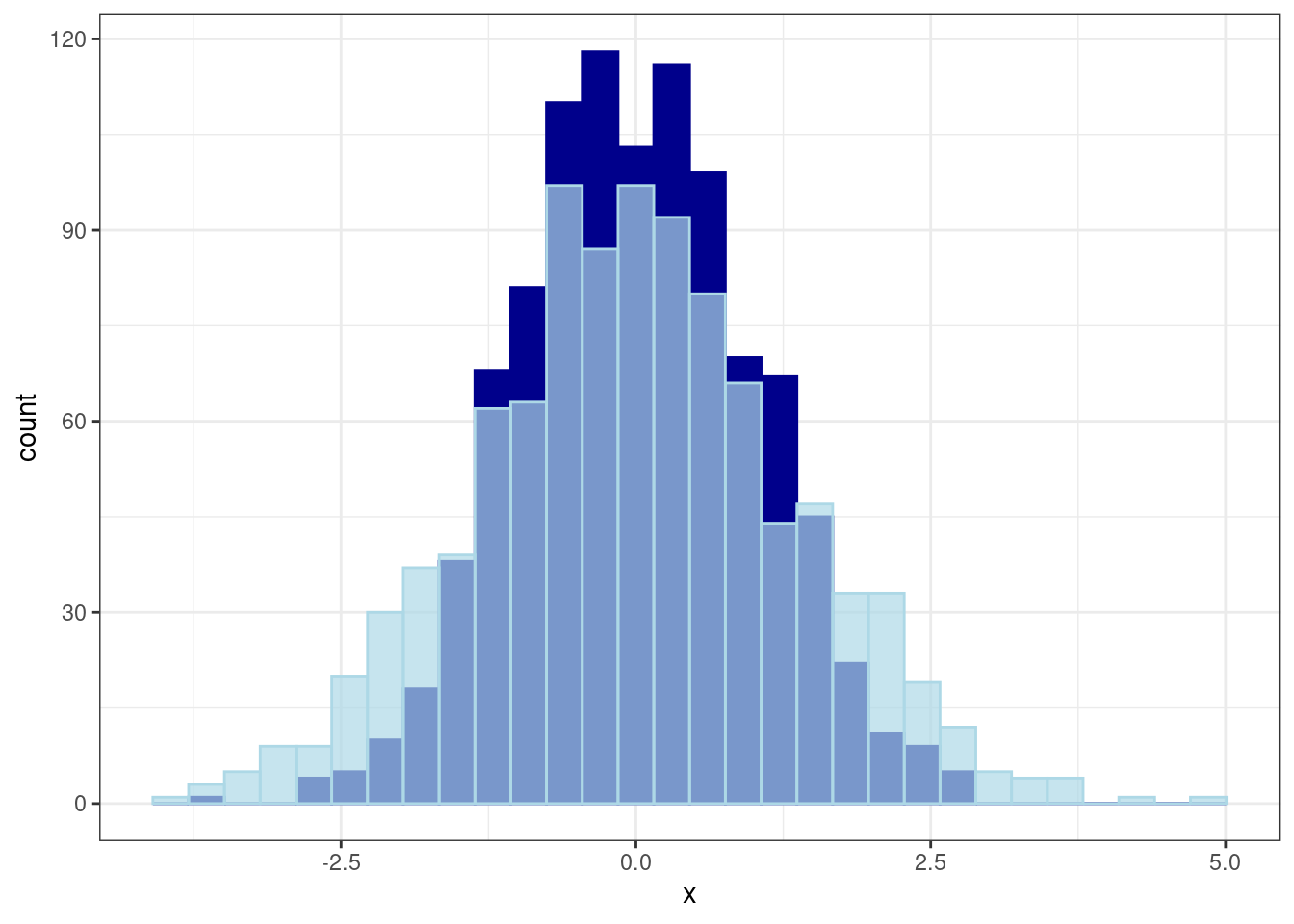

shapiro.test(x)

    Shapiro-Wilk normality test

data:  x
W = 0.99811, p-value = 0.3298
shapiro.test(y)

    Shapiro-Wilk normality test

data:  y
W = 0.99854, p-value = 0.5832

Zmienna x oraz y mają rozkład normalny.

18.4.2 Współczynnik korelacji

cor(df$x, df$y,
    use = "complete.obs",
    method = "pearson")
[1] 0.679556
cor(df$x, df$y,
    use = "complete.obs",
    method = "spearman")
[1] 0.6636062

Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?

18.4.3 Testy korelacji

cor.test(df$x, df$y,
    use = "complete.obs",
    method = "pearson")

    Pearson's product-moment correlation

data:  df$x and df$y
t = 29.263, df = 998, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.6447237 0.7115721
sample estimates:
     cor 
0.679556

Wynik testu korelacji wskazuje na istnieie istotnej korelacji między zmienną x oraz y.

18.5 Analiza korelacji - przykład

library(gapminder)
gapminder2007 = subset(gapminder, year == 2007)
gapminder2007_s = gapminder2007[c(4, 5, 6)]

Czy pomiędzy zmiennymi w zbiorze gapminder2007_s można dostrzec zależności liniowe?

library(ggplot2)
ggplot(gapminder2007_s, aes(lifeExp, gdpPercap)) + geom_point()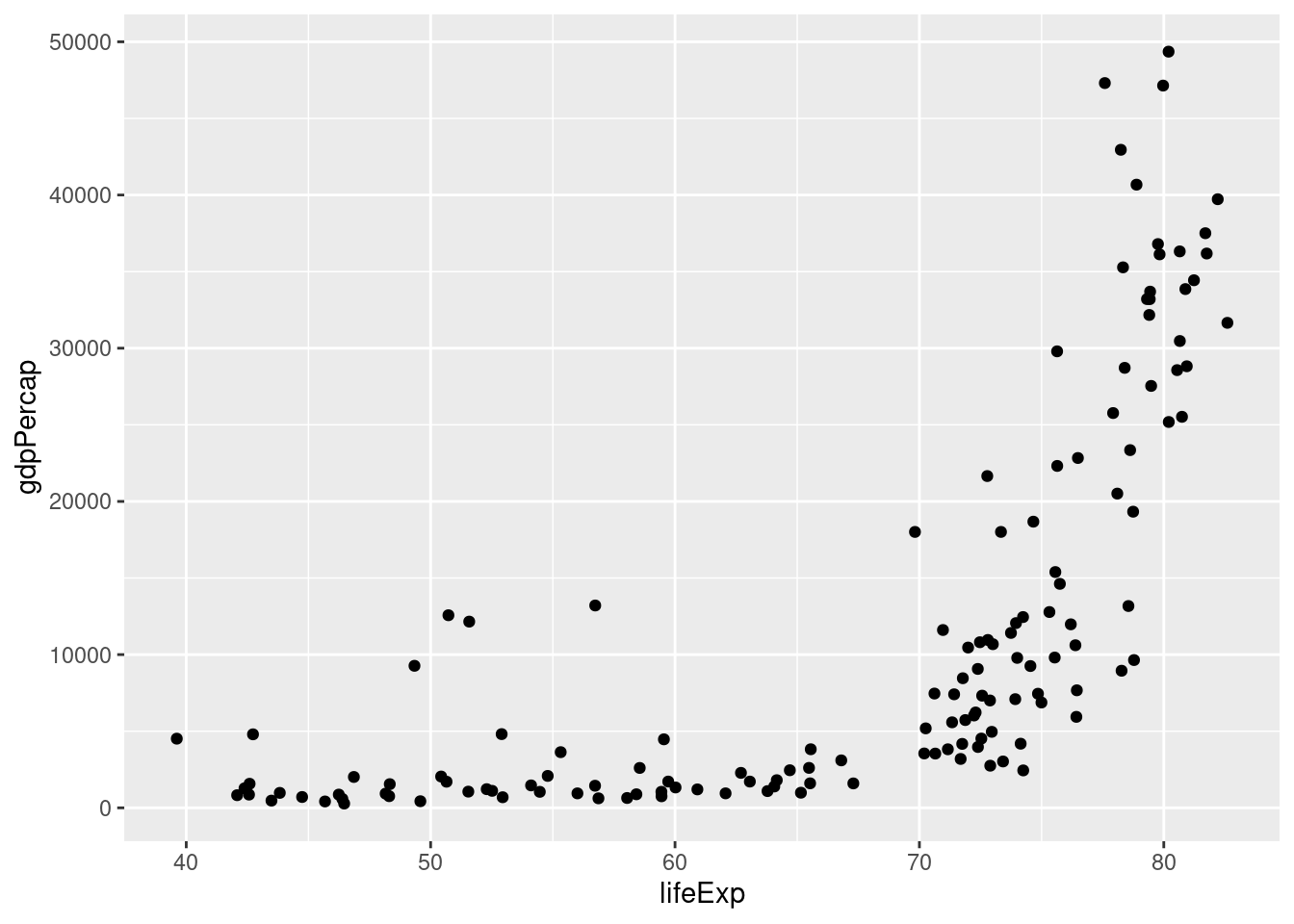

18.5.1 Współczynnik korelacji

cor(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
    use = "complete.obs",
    method = "pearson")
[1] 0.6786624
cor(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap, 
    use = "complete.obs",
    method = "spearman")
[1] 0.8565899

Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?

18.5.2 Testy korelacji

cor.test(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap, 
         use = "complete.obs",
         method = "pearson")

    Pearson's product-moment correlation

data:  gapminder2007_s$lifeExp and gapminder2007_s$gdpPercap
t = 10.933, df = 140, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.5786217 0.7585843
sample estimates:
      cor 
0.6786624 
cor.test(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
         use = "complete.obs",
         method = "spearman")

    Spearman's rank correlation rho

data:  gapminder2007_s$lifeExp and gapminder2007_s$gdpPercap
S = 68434, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.8565899

Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?

Używając danych z pakietu gapminder dla roku 1987 zwizualizuj relację pomiędzy populacją a oczekiwaną długością życia. Wylicz korelację i wykonaj odpowiedni test. Co oznacza jego wynik?

18.6 Określanie korelacji dla wielu zmiennych

18.6.1 Macierz wykresów korelacji

pairs(~lifeExp+gdpPercap+pop, data=gapminder2007_s, main="Simple Scatterplot Matrix")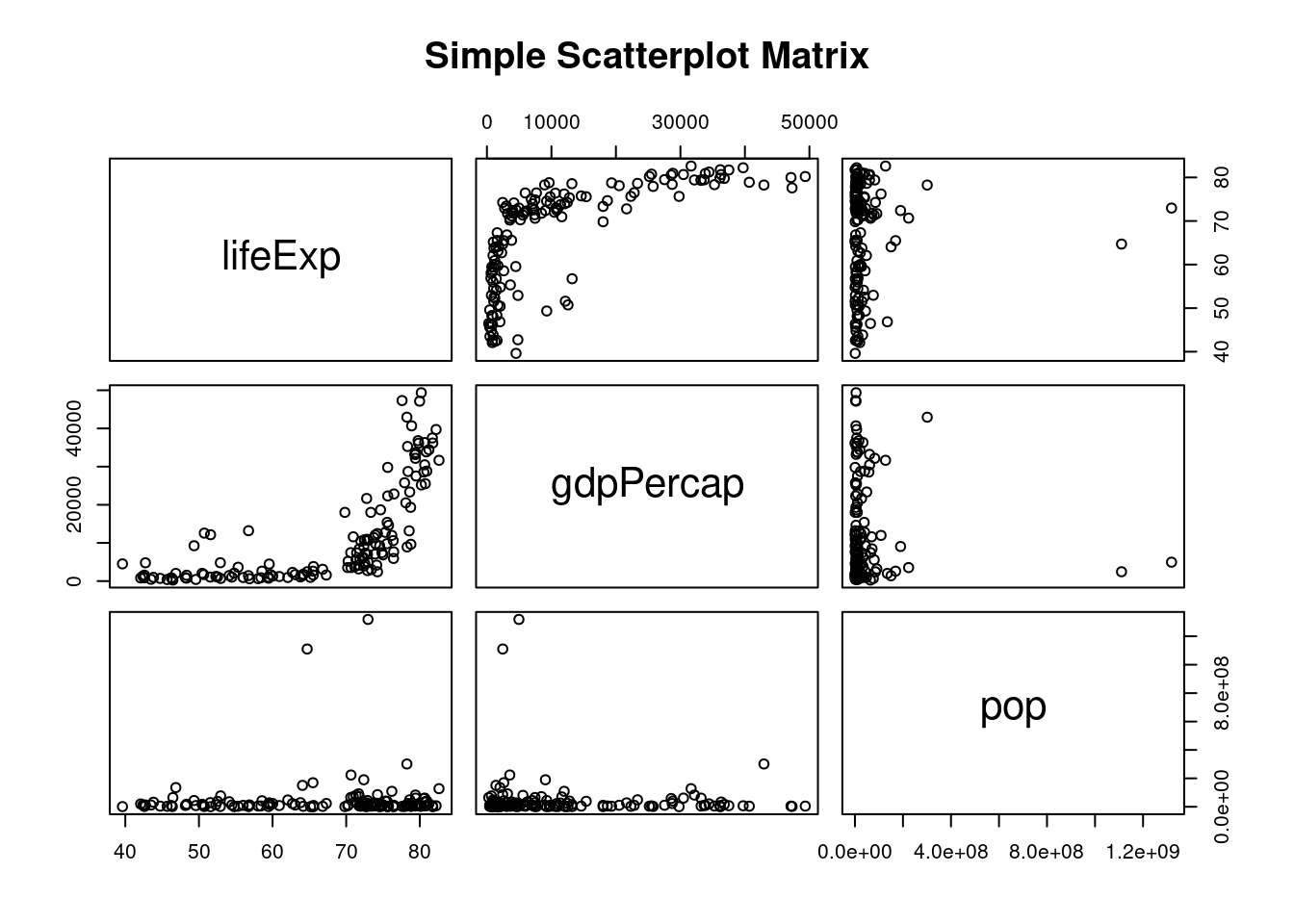

18.6.2 Macierz współczynników korelacji

Funkcja cor() pozwala na obliczenie macierzy współczynników korelacji. Podaje ona wartość współczynnika, ale nie wskazuje, czy wynik jest istotny statystycznie.

Funkcja rcorr() z pakietu Hmisc wyświetla zarówno macierz współczynników korelacji, jak i wartość p wskazującą czy wynik jest istotny statystycznie.

cor_spearman = cor(gapminder2007_s, 
                   use = "complete.obs",
                   method = "spearman")
round(cor_spearman , 4)
          lifeExp     pop gdpPercap
lifeExp    1.0000  0.0034    0.8566
pop        0.0034  1.0000   -0.0646
gdpPercap  0.8566 -0.0646    1.0000

W poniższym przykładzie pierwsza macierz zawiera współczynnik korelacji, druga liczbę obiektów a trzecia wartość poziomu istotności p. Wartość jest istotna statystycznie jeśli p jest mniejsze od założonego poziomu isotntości (np. 0,05)

library(Hmisc)
kor <- rcorr(as.matrix(gapminder2007_s), type = "spearman")
kor
          lifeExp   pop gdpPercap
lifeExp      1.00  0.00      0.86
pop          0.00  1.00     -0.06
gdpPercap    0.86 -0.06      1.00

n= 142 


P
          lifeExp pop    gdpPercap
lifeExp           0.9684 0.0000   
pop       0.9684         0.4451   
gdpPercap 0.0000  0.4451

18.7 Wizualizacja korelacji

  • Funkcja corrplot() z pakietu corrplot
library("corrplot")
kor <- rcorr(as.matrix(gapminder2007_s), type = "spearman")
corrplot(kor$r)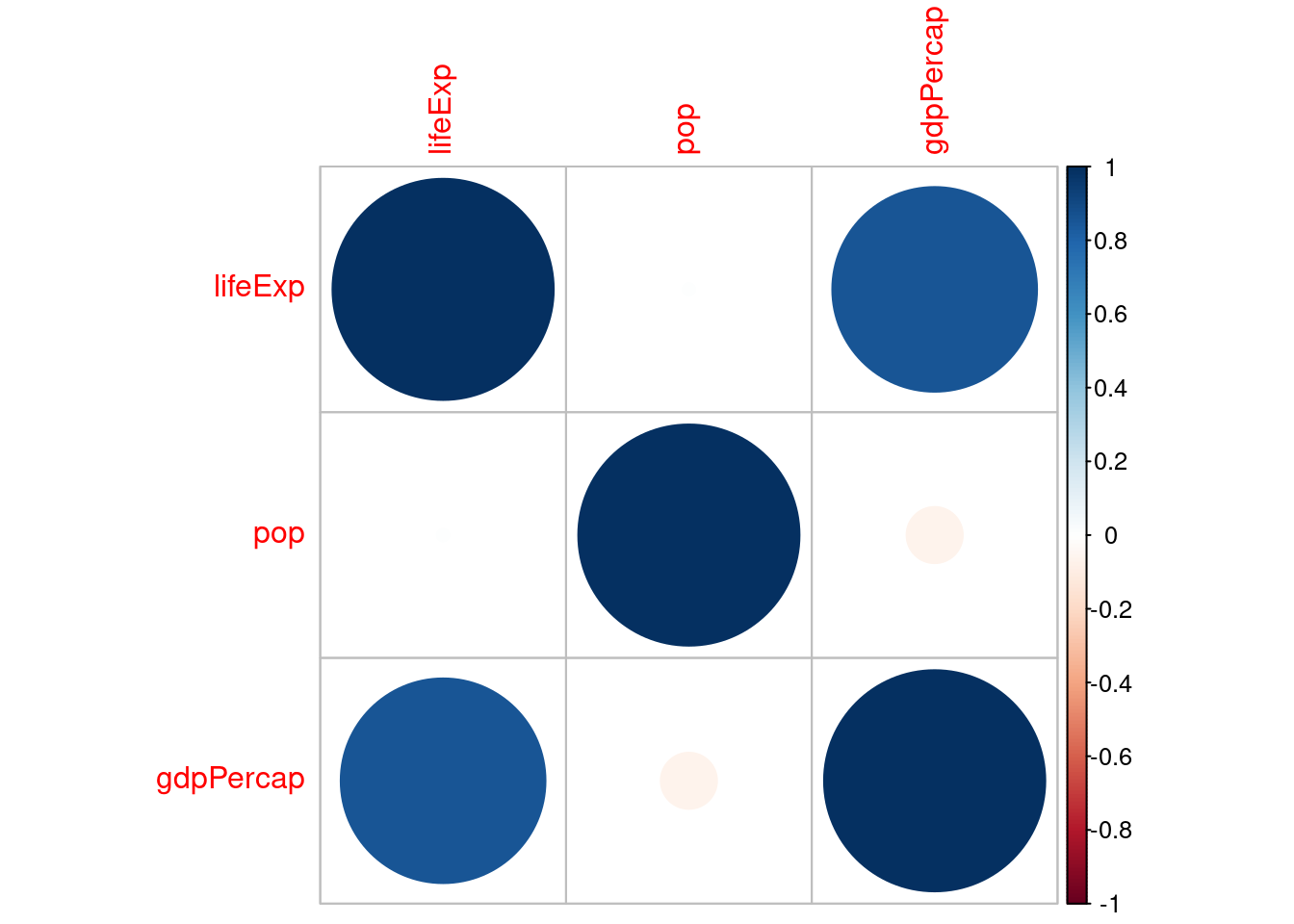

corrplot(kor$r, type = "upper", order = "hclust", 
         tl.col = "black", tl.srt = 45)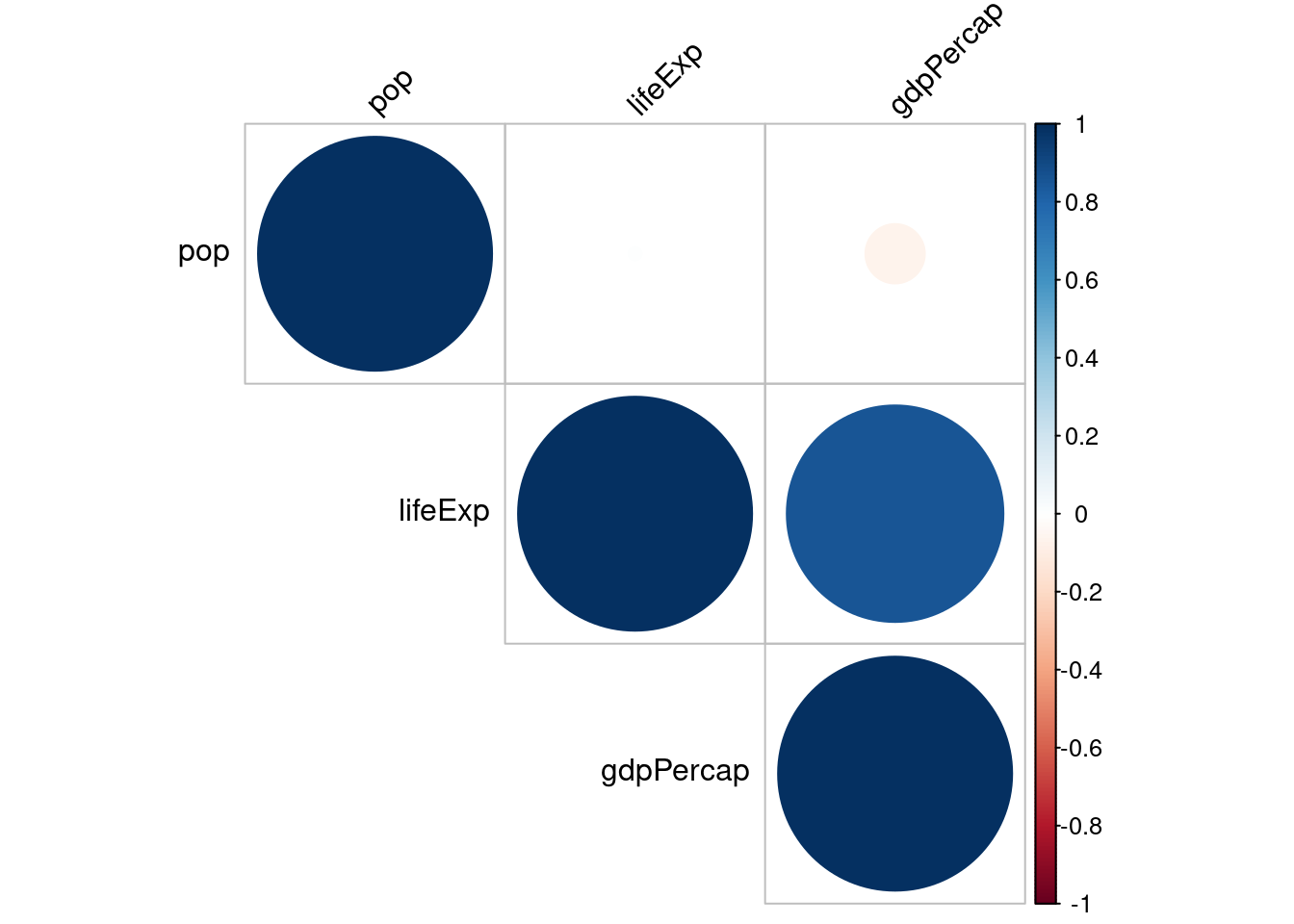

corrplot.mixed(kor$r, order="hclust", tl.col="black")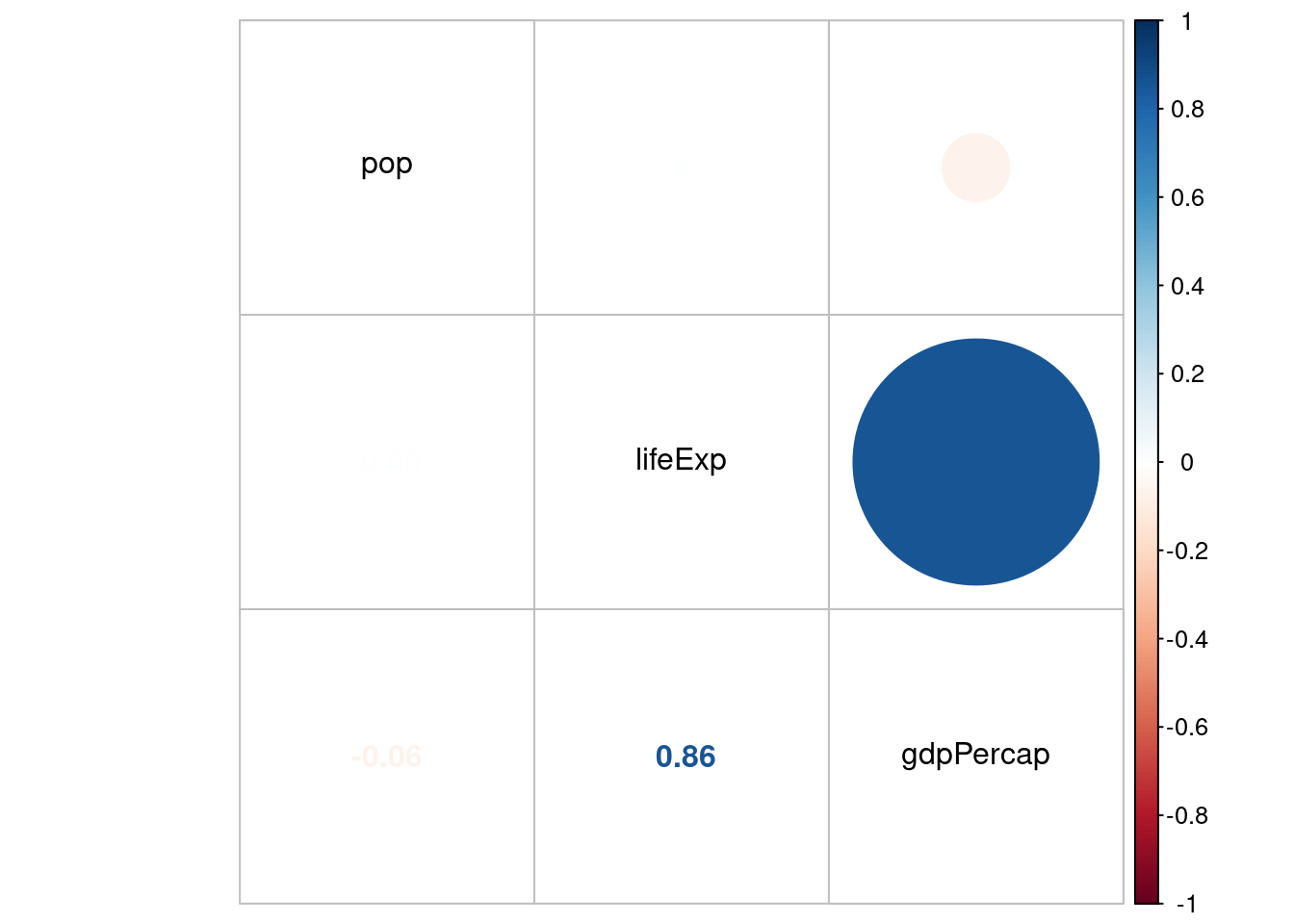

library(RColorBrewer)
corrplot(kor$r, type="upper", order="hclust", col=brewer.pal(n=8, name="RdYlBu"))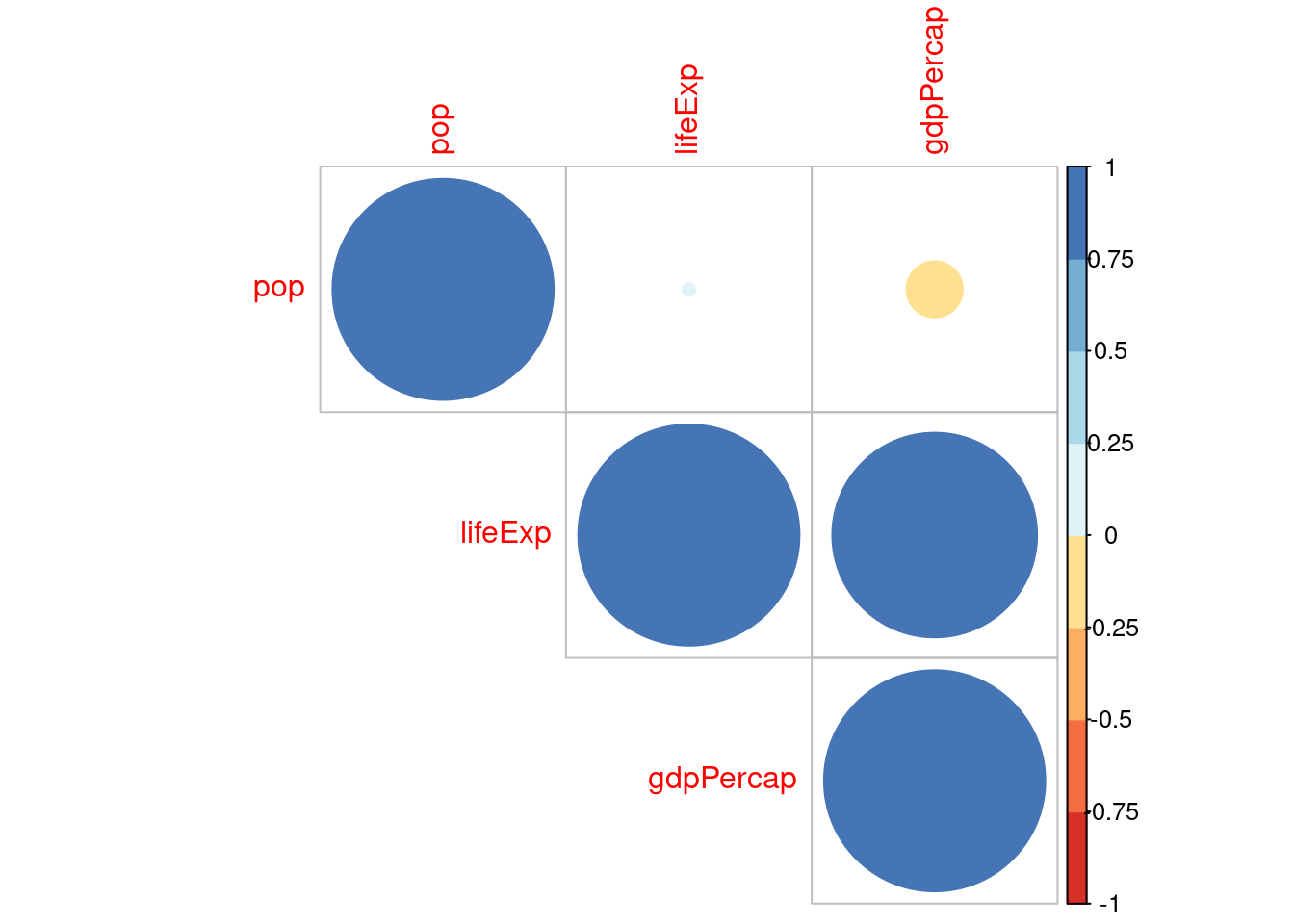

  • Funckja scatterplotMatrix() z pakietu car
library(car)
scatterplotMatrix(~lifeExp+gdpPercap+pop, data=gapminder2007_s)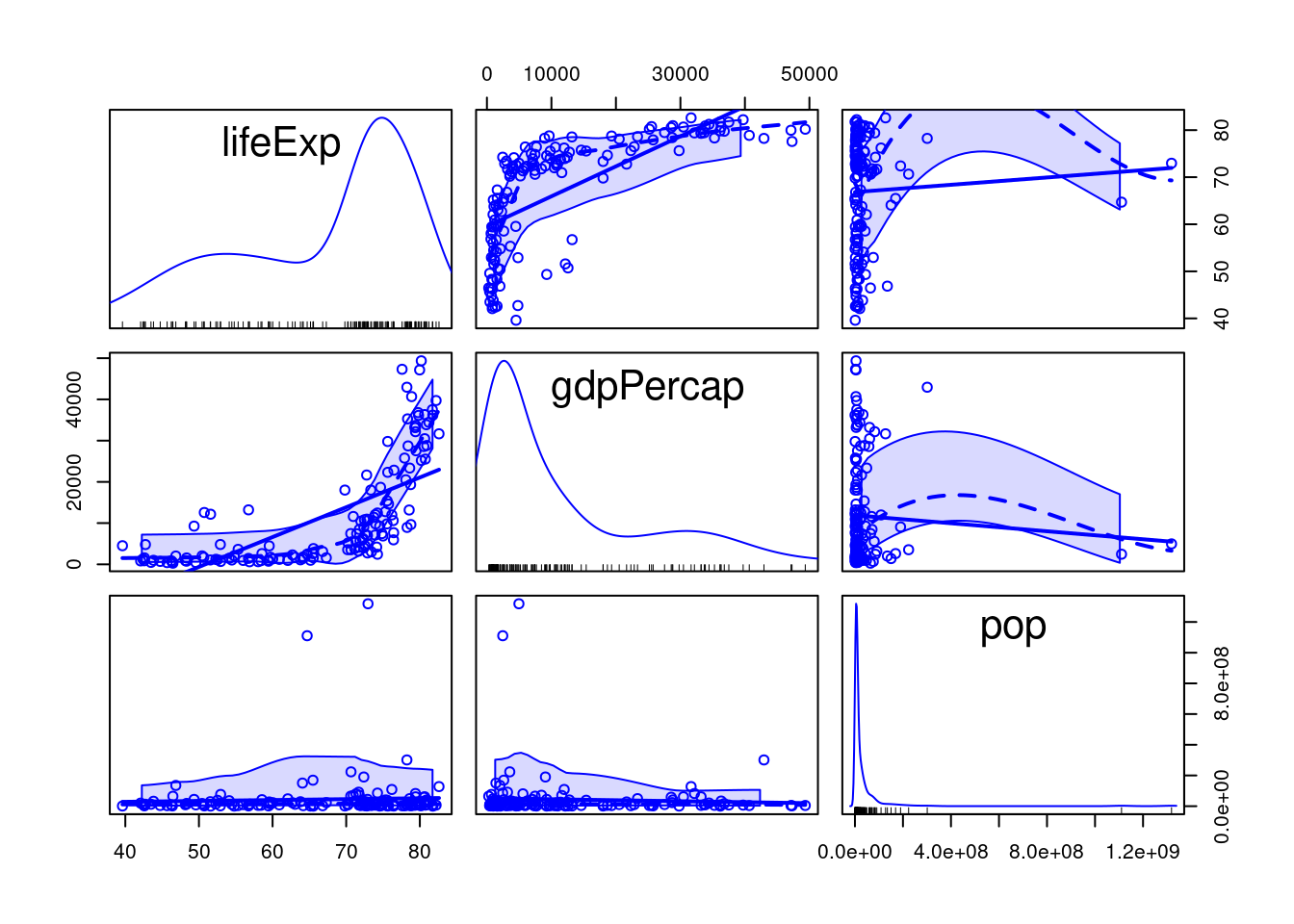

  • Funkcja chart.Correlation() z pakietu PerformanceAnalytics
library(PerformanceAnalytics)
chart.Correlation(gapminder2007_s, histogram=TRUE, pch=19, method = "spearman")
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter
Warning in par(usr): argument 1 does not name a graphical parameter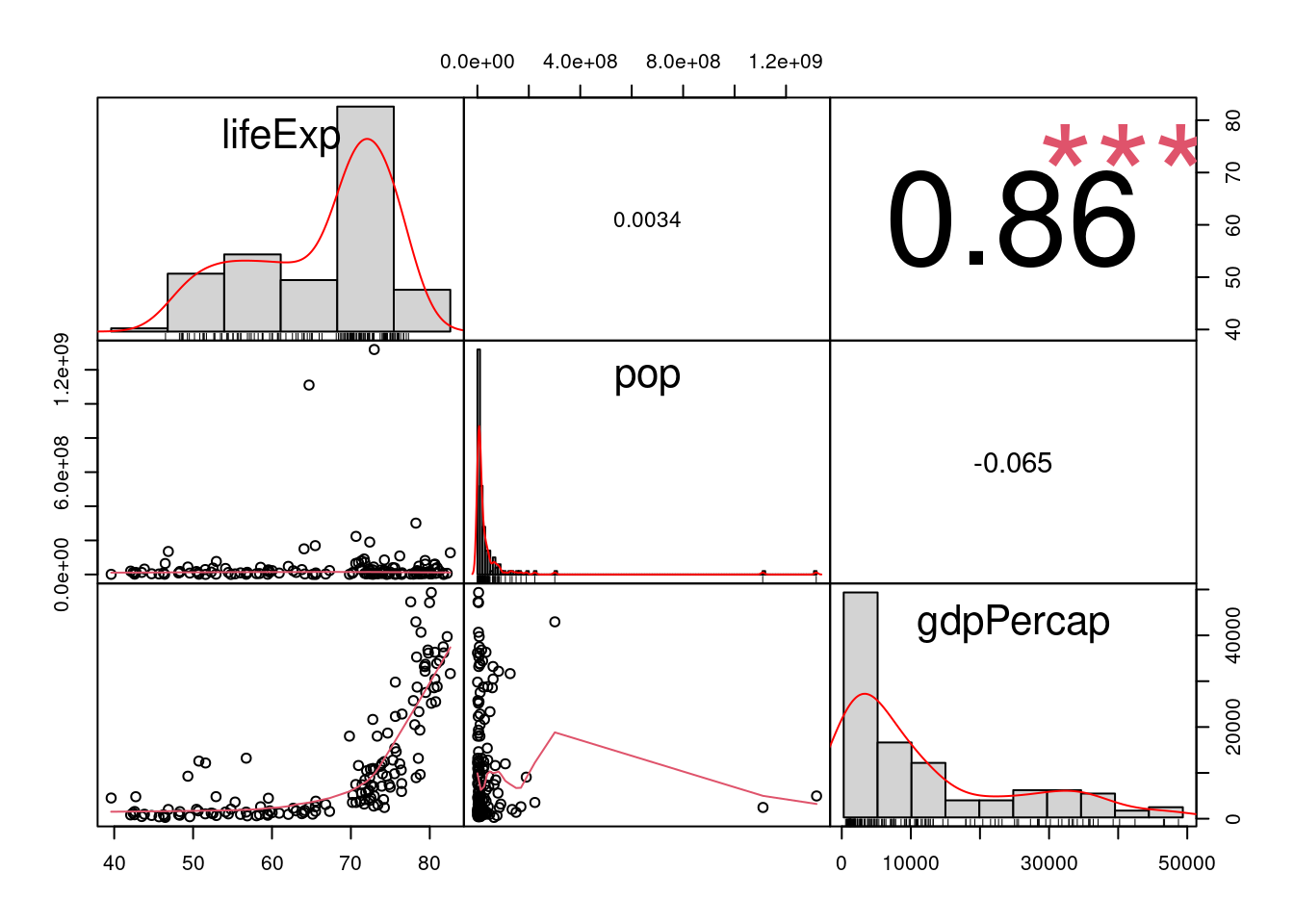

  • Funkcja pairs.panels() z pakietu psych
library(psych)
pairs.panels(gapminder2007_s, scale=TRUE)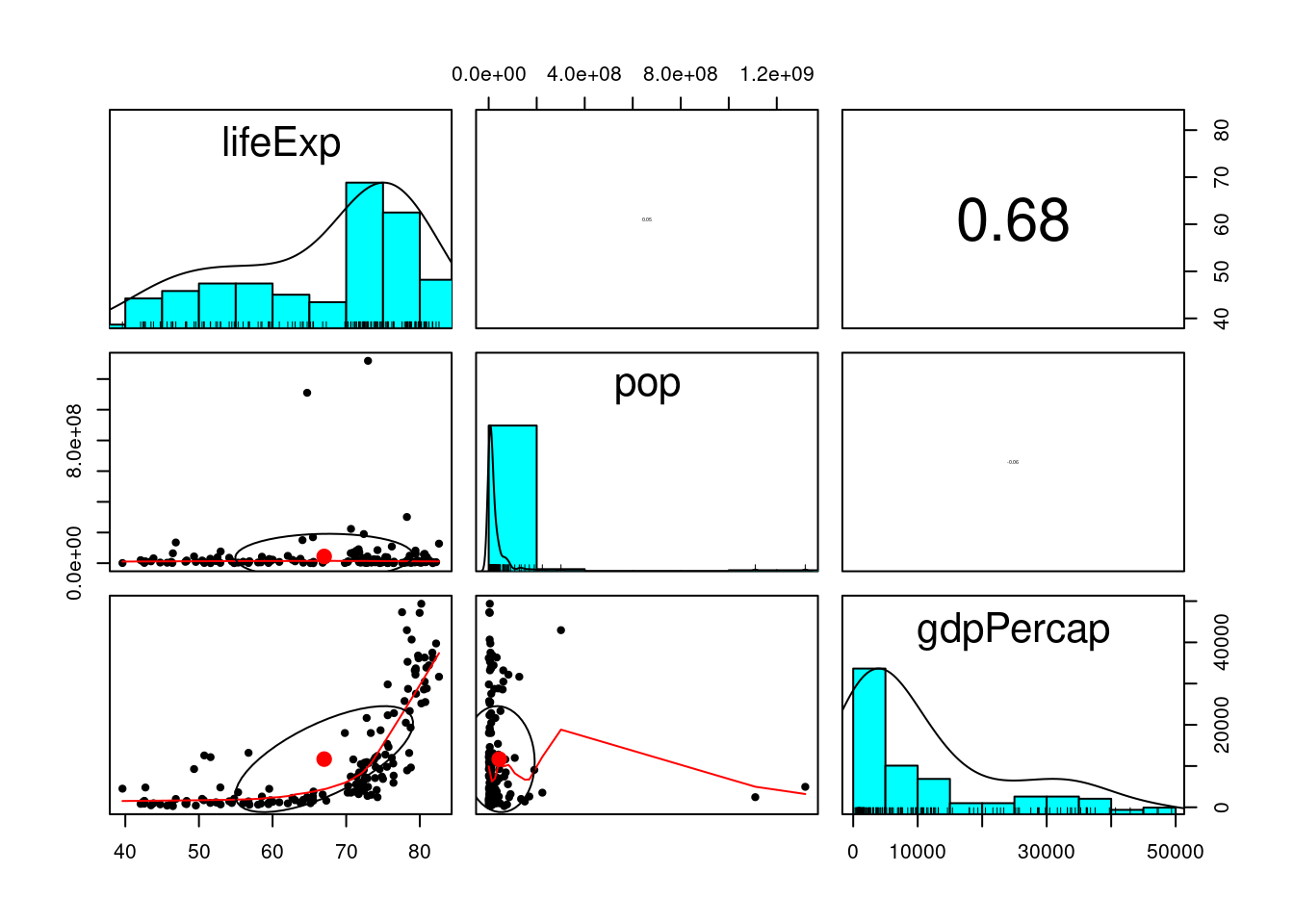

  • Funkcja ggcorr() i ggpairs() z pakietu GGally
library(GGally)
ggcorr(gapminder2007_s, nbreaks=8, palette='RdGy', label=TRUE, label_size=5, label_color='white')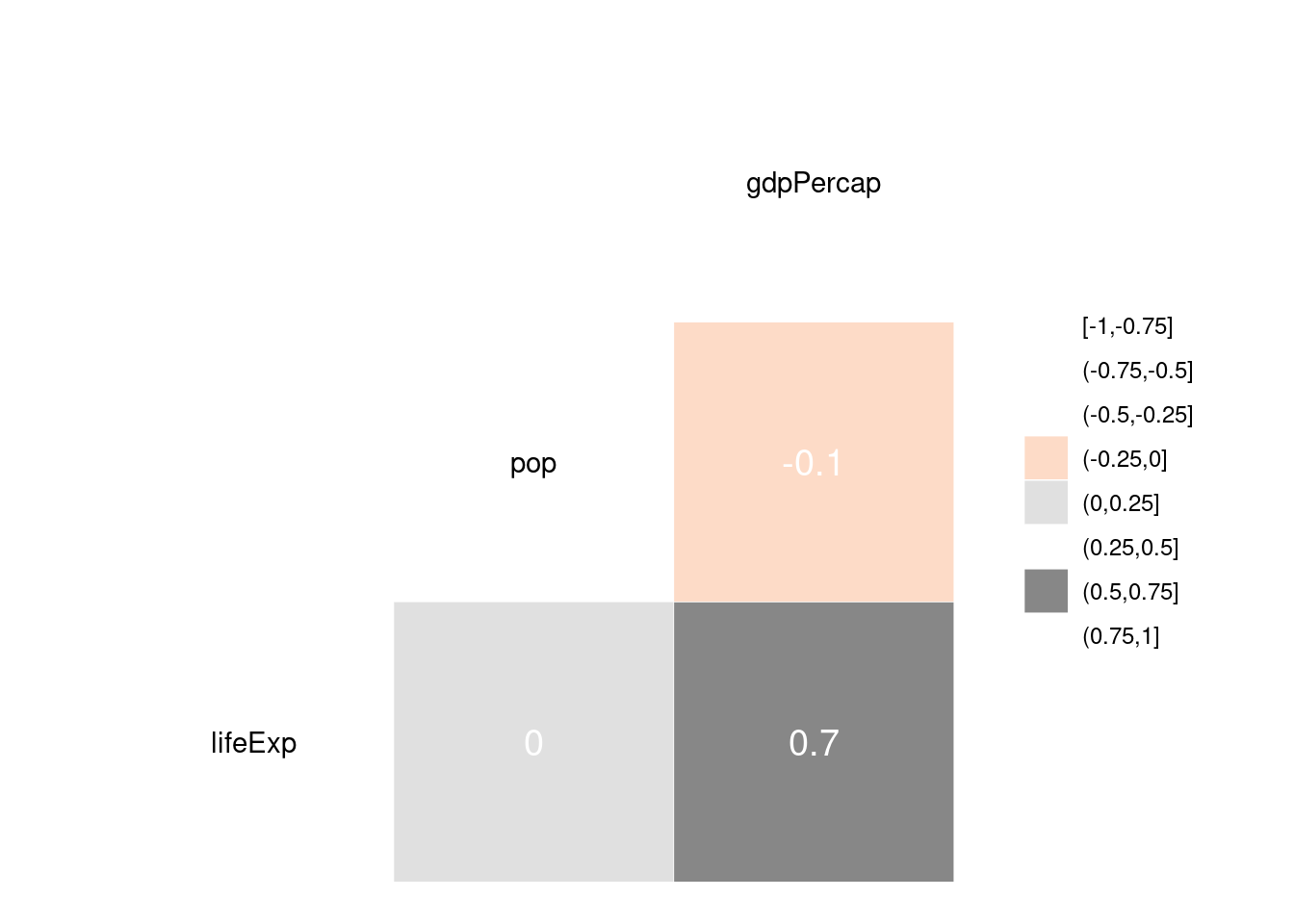

library(GGally)
ggpairs(gapminder2007_s)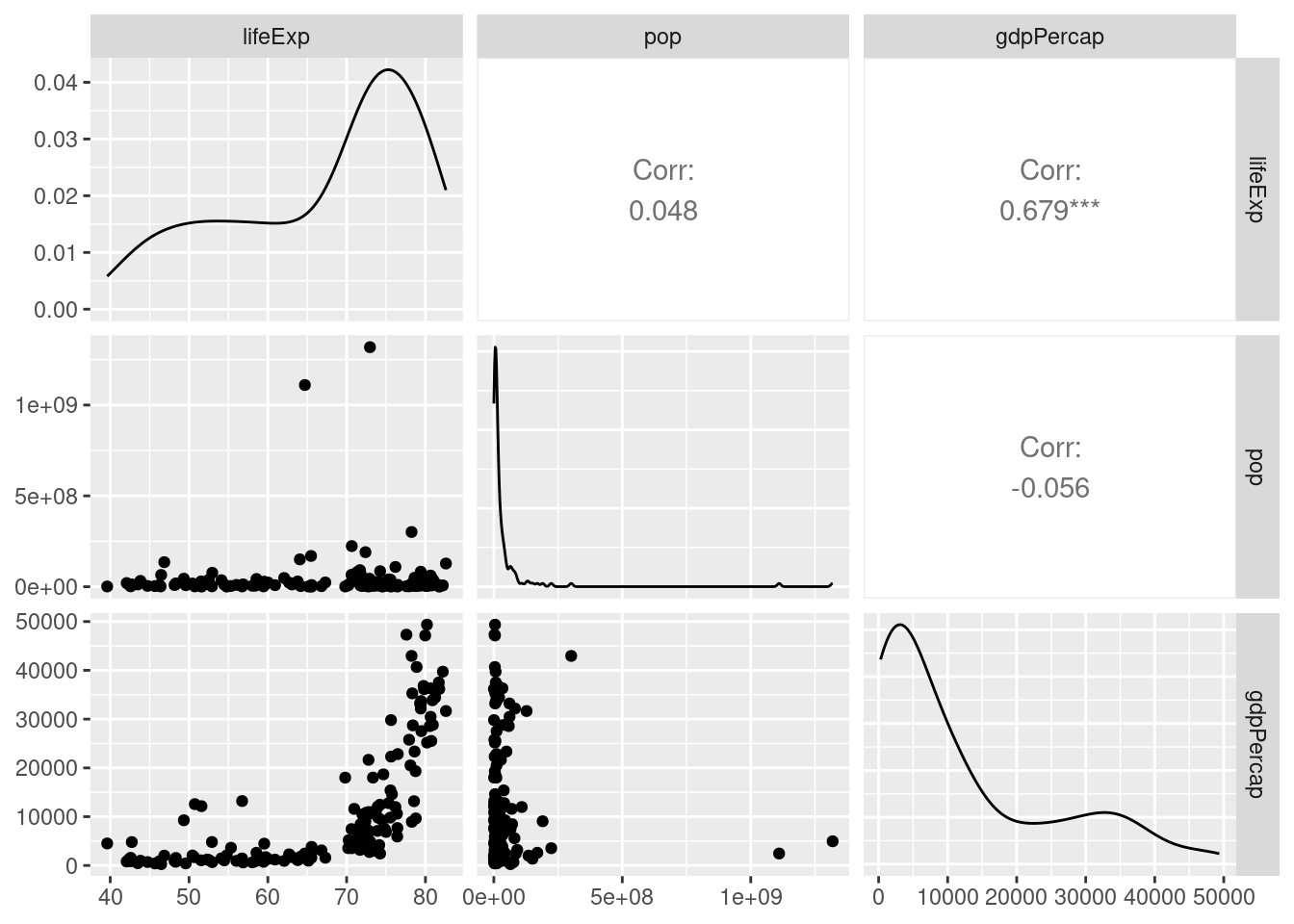

Używając danych z pakietu gapminder dla roku 1987 zwizualizuj relację pomiędzy zmiennymi populacją (pop), oczekiwaną długością życia (lifeExp) i PKB (gdPercap). Wylicz korelację. Co oznacza wynik?