18 Analiza korelacji
18.1 Wprowadzenie
18.1.1 Podstawowe pojęcia
Analiza korelacji służy do “wychwycenia” czy zachodzi związek pomiędzy dwiema (lub więcej) zmiennymi.
Miarą korelacji jest współczynnik korelacji
Współczynnik korelacji dostarcza informacji o tym jaka jest siła związku (wartość współczynnika) oraz jaki jest kierunek związku (znak).
Dla każdego współczynnika korelacji należy także obliczyć jego istotność statystyczną, stosujac jeden z testów istotności przeznaczonych dla współczynników korelacji.
- Hipoteza zerowa: ρ x,y=0
- Hipoteza alternatywna: ρ x,y≠0 lub ρ x,y<0 lub ρ x,y>0
Zależność między zmiennymi może mieć charakter liniowy lub krzywoliniowy.
18.1.2 Korelacja a przyczynowość
Korelacja nie wskazuje na istnienie związku przyczynowo-skutkowego pomiędzy zmiennymi.
Innymi słowy: Istnienie korelacji liczbowej nie potwierdza, że jedno zjawisko powoduje drugie.
- A może powodować B
- B może powodować A
- A lub B może być wywołane przez C
- Zależność między A i B może być przypadkowa.
18.1.3 Kilka ważnych informacji
- Najważniejsza jest isotność korelacji. Niepotrzebna nam korelacja nawet bardzo wysoka, jeśli nie jest istotna statystycznie.
- Wartość współczynnika nawet bliska 0 nie zawsze oznacza brak zależności. Może oznaczać jedynie brak zależności liniowej.
- Wielkość współczynnika podlega wpływom wartości skrajnych i odstających.
18.1.4 Korelacja liniowa
Miarą korelacji liniowej jest współczynnik korelacji Pearsona.
Współczynniki korelacji przyjmują wartości z przedziału od -1,00 do +1,00.
Wartość -1,00 - reprezentuje doskonałą korelację ujemną (współzależność pomiędzy zmiennymi kształtująca się w taki sposób, że gdy wartości jednej zmiennej wykazują tendencję rosnącą, wówczas wartości drugiej zmiennej wykazują tendencję malejącą)
wartość +1,00 - reprezentuje doskonałą korelacją dodatnią (współzależność pomiędzy zmiennymi przedstawia się w taki sposób, że gdy wartości jednej zmiennej wykazują tendencję wzrastającą, wówczas wartości drugiej zmiennej także wykazują tendencję wzrastającą).
Wartość 0.00 wyraża brak korelacji.
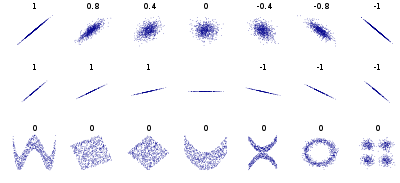
18.1.5 Jak silna jest korelacja?
Do opisu i interpretacji istotnej korelacji pomocne może być przyjęcie pewnej skali określającą siłę związku. Nie ma jednej przyjętej skali. Poniżej przedstawiam jedną z nich:
- 0 - brak korelacji
- 0,1 do 0,3 - słaba korelacja
- 0,3 do 0,5 - przeciętna korelacja
- 0,5 do 0,7 - korelacja wysoka
- 0,7 do 0,9 - korelacja bardzo wysoka
- 0,9 do 1 - korelacja prawie pełna
18.2 Demonstracja dla współczynnika korelacji liniowej
install.packages("TeachingDemos")
library("TeachingDemos")
put.points.demo(x = NULL, y = NULL, lsline = TRUE)
#Używając opcji Add Point dodaj punkty w oknie wykresu
#Zwróć uwagę jak zmienia się wartość współczynnika korelacji (r). Zgadnij wartość współczynnika korelacji - https://gallery.shinyapps.io/correlation_game/
18.3 Testy korelacji
test korelacji liniowej Pearsona
- stosowany gdy zmienne mają zależnośc liniową
- zmienne mają rozkład normalny
test korelacji rang Spearman
- stosowany gdy naruszone jest założenie o normalności rozkładu (np. gdy istnieją wartości odstające)
18.4 Korelacja liniowa
set.seed(25)
x = rnorm(1000)
y = x + rnorm(1000)
df = data.frame(x, y)library(ggplot2)
ggplot(df, aes(x, y)) + geom_point() + stat_smooth(method = lm)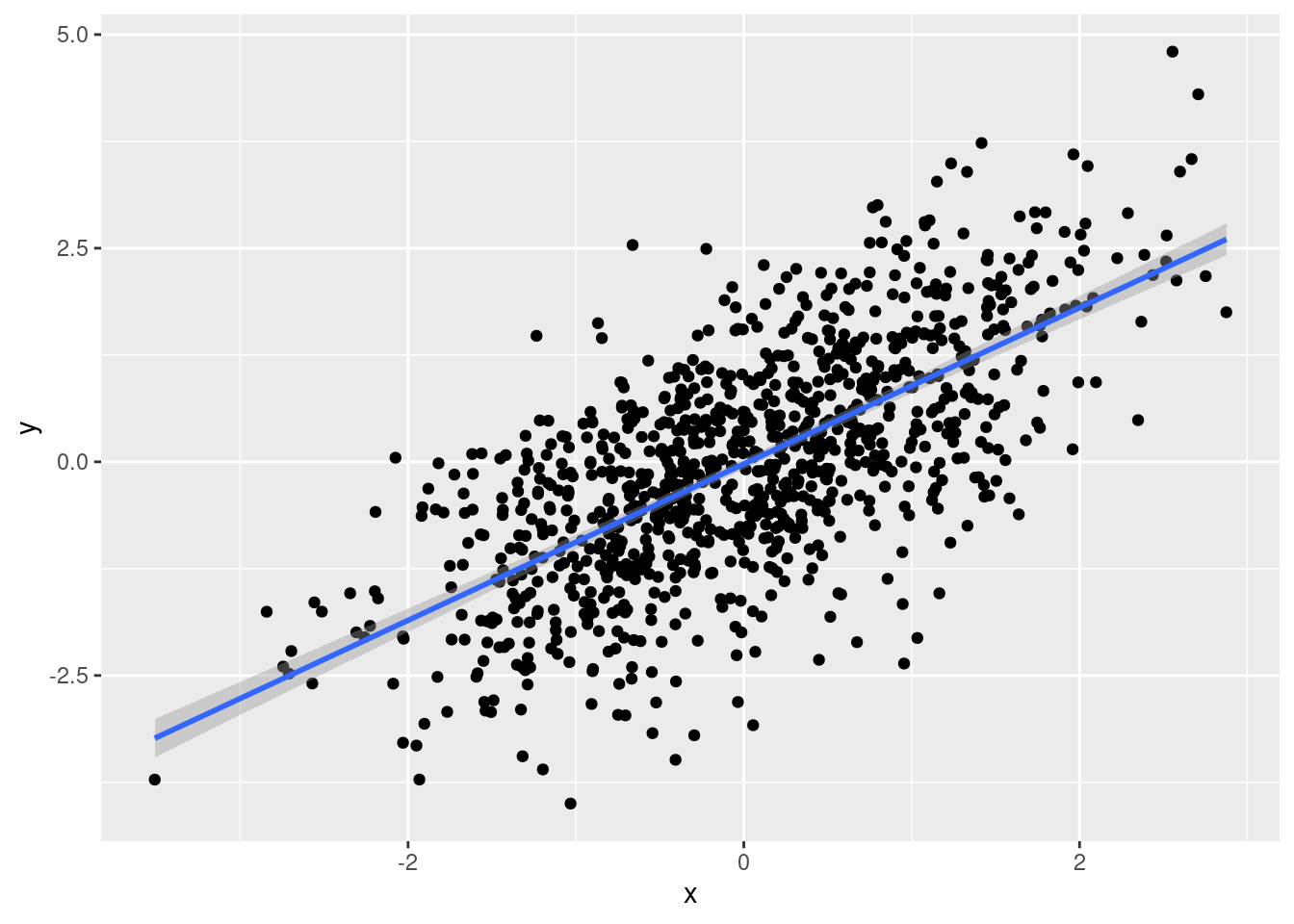
18.4.1 Zbadanie normalności rozkładu
ggplot(df) +
geom_histogram(aes(x = x), col = "darkblue", fill = "darkblue") +
geom_histogram(aes(x = y), col = "lightblue", fill = "lightblue", alpha = 0.7) +
theme_bw()`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.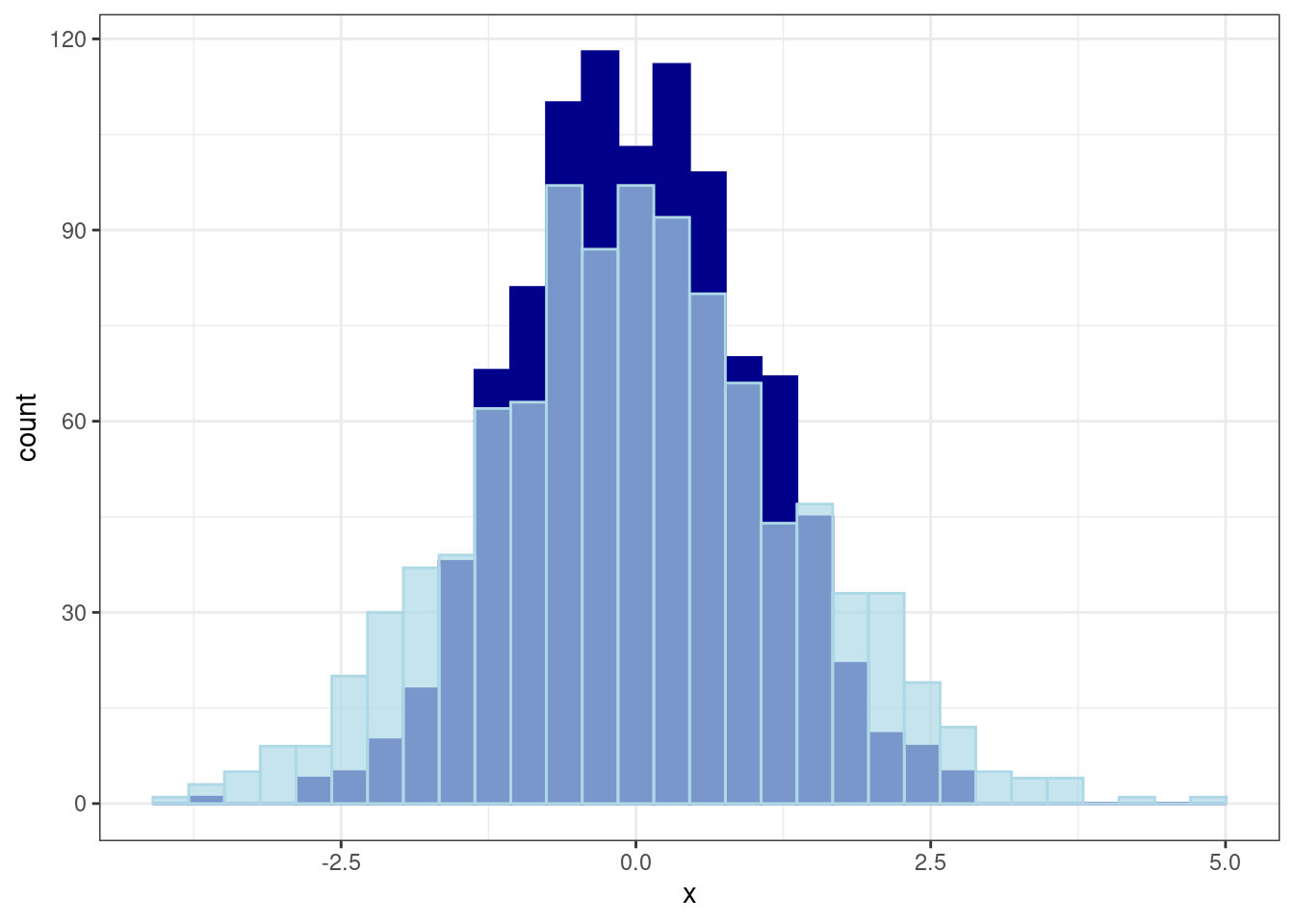
shapiro.test(x)
Shapiro-Wilk normality test
data: x
W = 0.99811, p-value = 0.3298shapiro.test(y)
Shapiro-Wilk normality test
data: y
W = 0.99854, p-value = 0.5832Zmienna x oraz y mają rozkład normalny.
18.4.2 Współczynnik korelacji
cor(df$x, df$y,
use = "complete.obs",
method = "pearson")[1] 0.679556cor(df$x, df$y,
use = "complete.obs",
method = "spearman")[1] 0.6636062Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?
18.4.3 Testy korelacji
cor.test(df$x, df$y,
use = "complete.obs",
method = "pearson")
Pearson's product-moment correlation
data: df$x and df$y
t = 29.263, df = 998, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.6447237 0.7115721
sample estimates:
cor
0.679556 Wynik testu korelacji wskazuje na istnieie istotnej korelacji między zmienną x oraz y.
18.5 Analiza korelacji - przykład
library(gapminder)
gapminder2007 = subset(gapminder, year == 2007)
gapminder2007_s = gapminder2007[c(4, 5, 6)]Czy pomiędzy zmiennymi w zbiorze gapminder2007_s można dostrzec zależności liniowe?
library(ggplot2)
ggplot(gapminder2007_s, aes(lifeExp, gdpPercap)) + geom_point()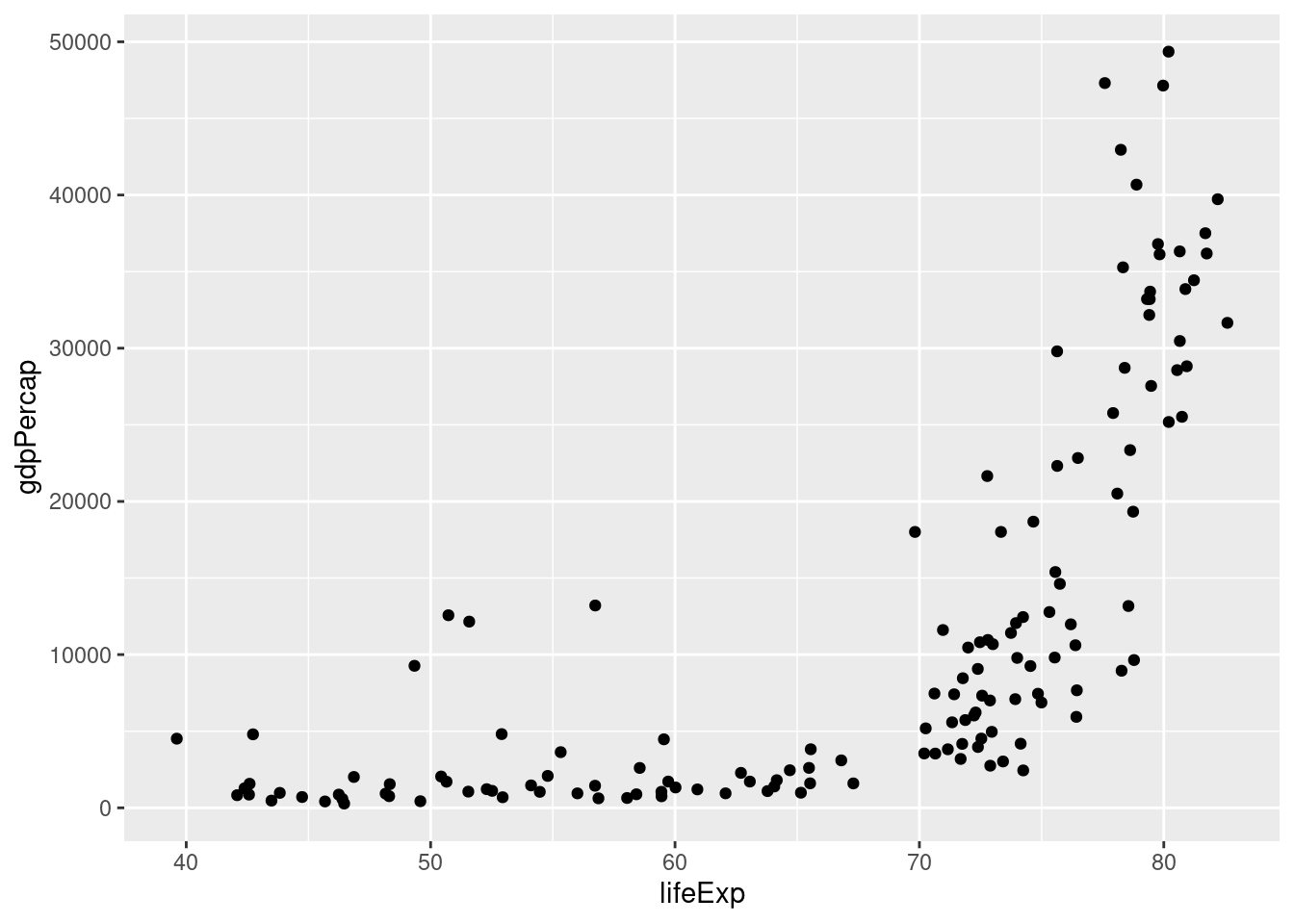
18.5.1 Współczynnik korelacji
cor(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
use = "complete.obs",
method = "pearson")[1] 0.6786624cor(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
use = "complete.obs",
method = "spearman")[1] 0.8565899Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?
18.5.2 Testy korelacji
cor.test(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
use = "complete.obs",
method = "pearson")
Pearson's product-moment correlation
data: gapminder2007_s$lifeExp and gapminder2007_s$gdpPercap
t = 10.933, df = 140, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5786217 0.7585843
sample estimates:
cor
0.6786624 cor.test(gapminder2007_s$lifeExp, gapminder2007_s$gdpPercap,
use = "complete.obs",
method = "spearman")
Spearman's rank correlation rho
data: gapminder2007_s$lifeExp and gapminder2007_s$gdpPercap
S = 68434, p-value < 2.2e-16
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.8565899 Która metoda korelacji powinna zostać użyta - korelacja liniowa Pearsona, czy korelacja rang Spearmana? Dlaczego?
Używając danych z pakietu gapminder dla roku 1987 zwizualizuj relację pomiędzy populacją a oczekiwaną długością życia. Wylicz korelację i wykonaj odpowiedni test. Co oznacza jego wynik?
Rozwiązanie:
W przykładzie należy obliczyć współczynnik korelacji Spearmana. Wynik wskazuje na brak kolelacji między zmiennymi. Współczynnik korelacji nie jest istotny statystycznie.
gapminder87 <- filter(gapminder, year == 1987)
ggplot(gapminder87, aes(pop, lifeExp)) + geom_point()
cor.test(gapminder87$lifeExp, gapminder87$pop,
use = "complete.obs",
method = "spearman")18.6 Określanie korelacji dla wielu zmiennych
18.6.1 Macierz wykresów korelacji
pairs(~lifeExp+gdpPercap+pop, data=gapminder2007_s, main="Simple Scatterplot Matrix")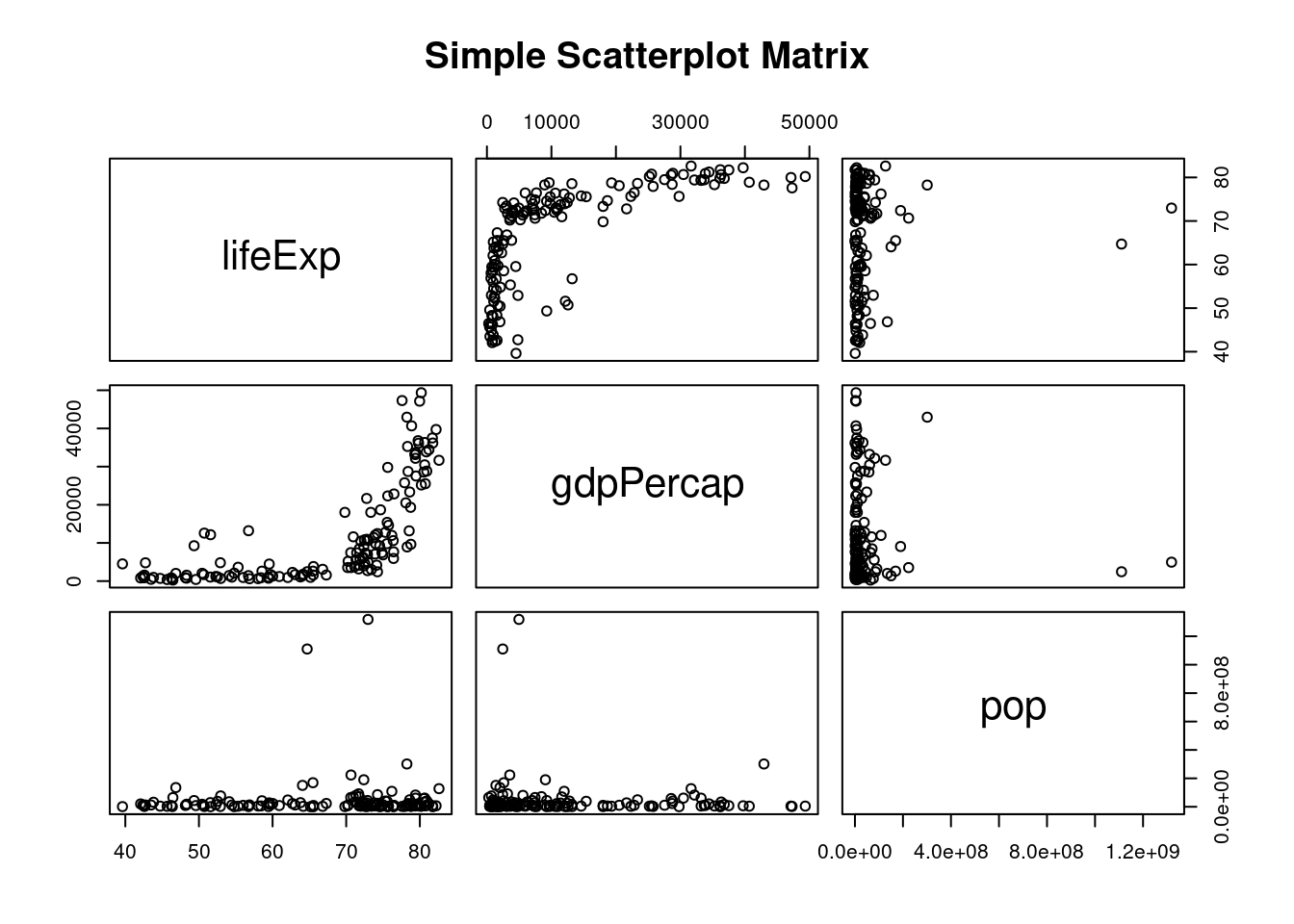
18.6.2 Macierz współczynników korelacji
Funkcja cor() pozwala na obliczenie macierzy współczynników korelacji. Podaje ona wartość współczynnika, ale nie wskazuje, czy wynik jest istotny statystycznie.
Funkcja rcorr() z pakietu Hmisc wyświetla zarówno macierz współczynników korelacji, jak i wartość p wskazującą czy wynik jest istotny statystycznie.
cor_spearman = cor(gapminder2007_s,
use = "complete.obs",
method = "spearman")
round(cor_spearman , 4) lifeExp pop gdpPercap
lifeExp 1.0000 0.0034 0.8566
pop 0.0034 1.0000 -0.0646
gdpPercap 0.8566 -0.0646 1.0000W poniższym przykładzie pierwsza macierz zawiera współczynnik korelacji, druga liczbę obiektów a trzecia wartość poziomu istotności p. Wartość jest istotna statystycznie jeśli p jest mniejsze od założonego poziomu isotntości (np. 0,05)
library(Hmisc)
kor <- rcorr(as.matrix(gapminder2007_s), type = "spearman")
kor lifeExp pop gdpPercap
lifeExp 1.00 0.00 0.86
pop 0.00 1.00 -0.06
gdpPercap 0.86 -0.06 1.00
n= 142
P
lifeExp pop gdpPercap
lifeExp 0.9684 0.0000
pop 0.9684 0.4451
gdpPercap 0.0000 0.4451 18.7 Wizualizacja korelacji
- Funkcja
corrplot()z pakietucorrplot
library("corrplot")
kor <- rcorr(as.matrix(gapminder2007_s), type = "spearman")
corrplot(kor$r)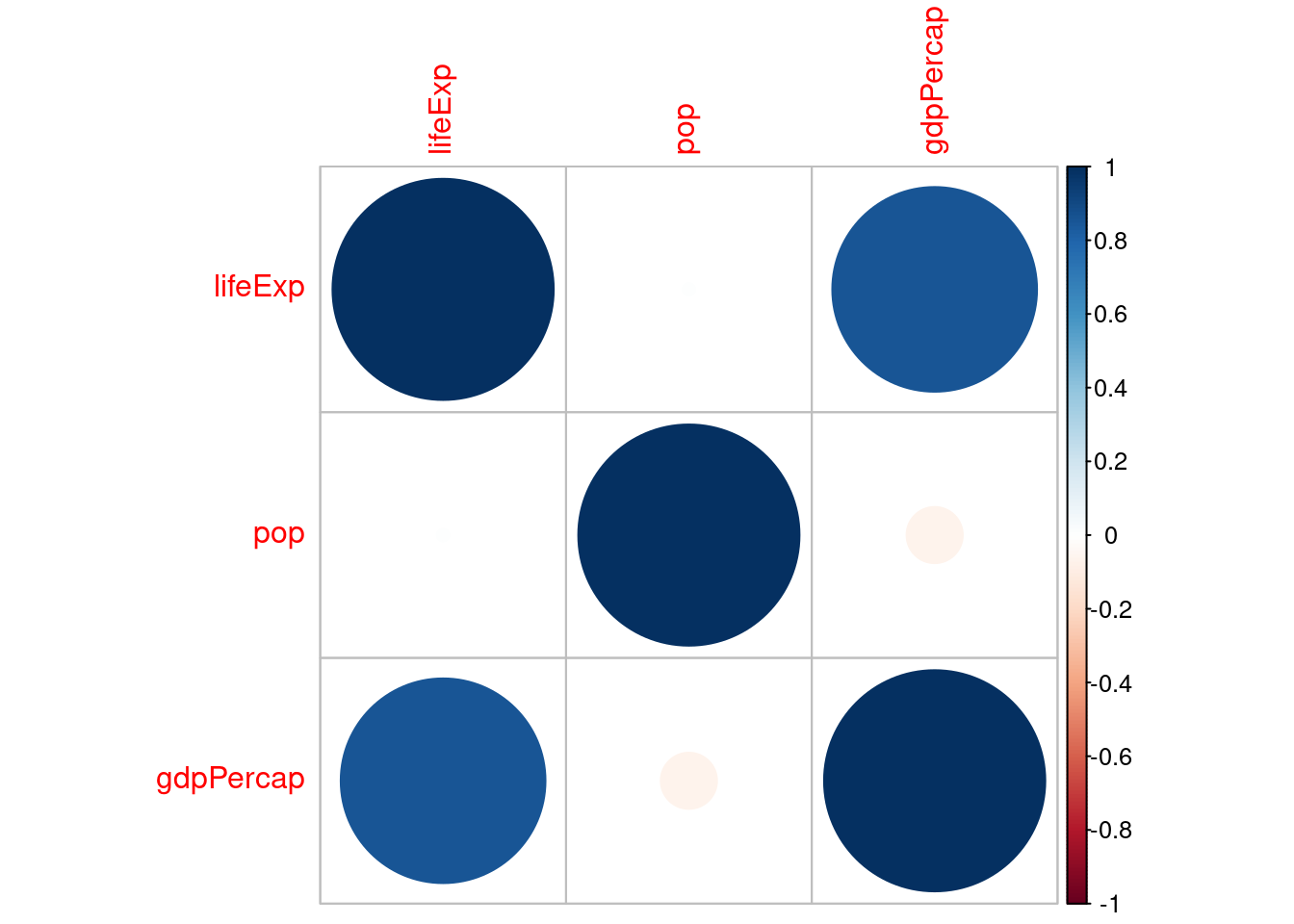
corrplot(kor$r, type = "upper", order = "hclust",
tl.col = "black", tl.srt = 45)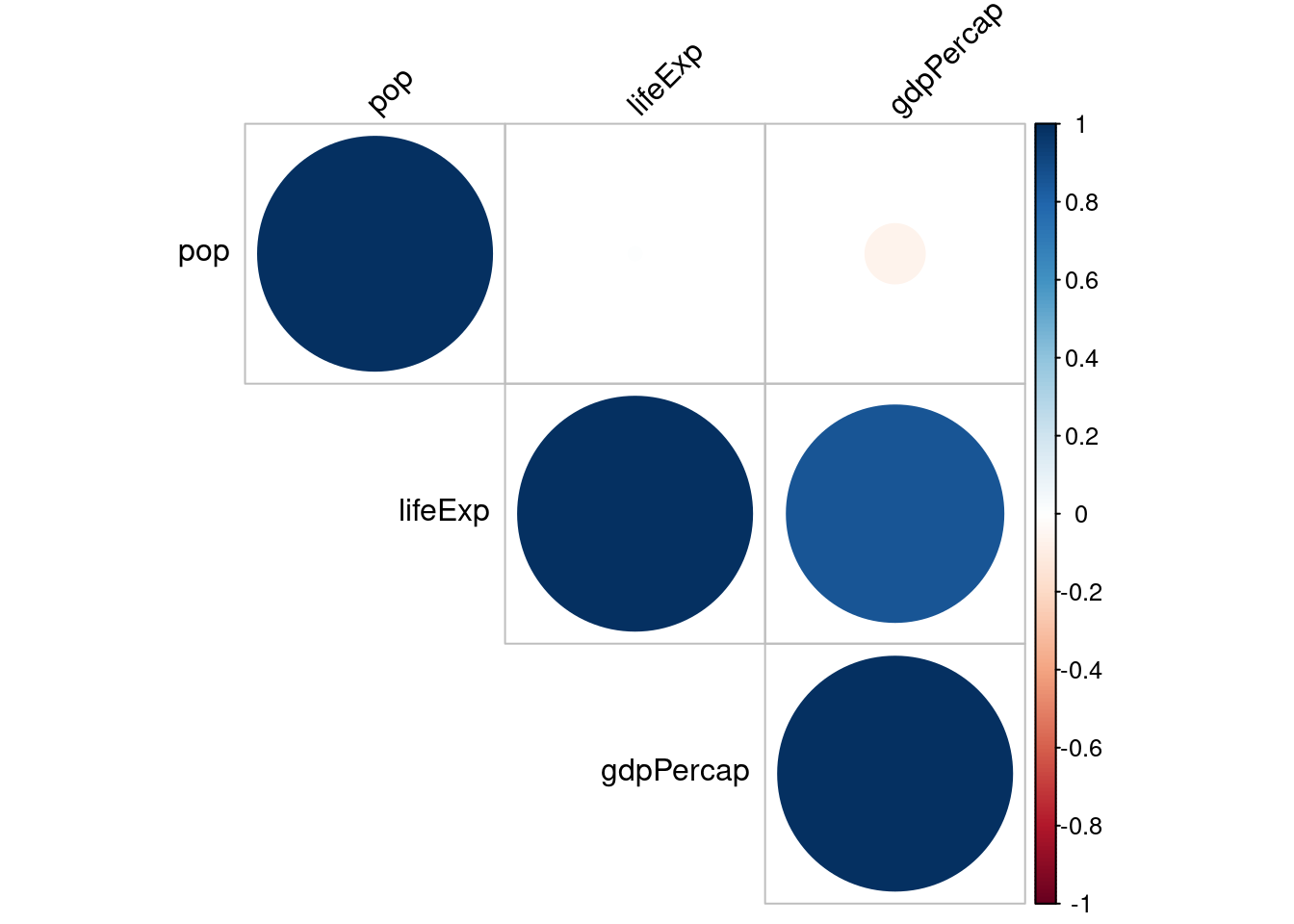
corrplot.mixed(kor$r, order="hclust", tl.col="black")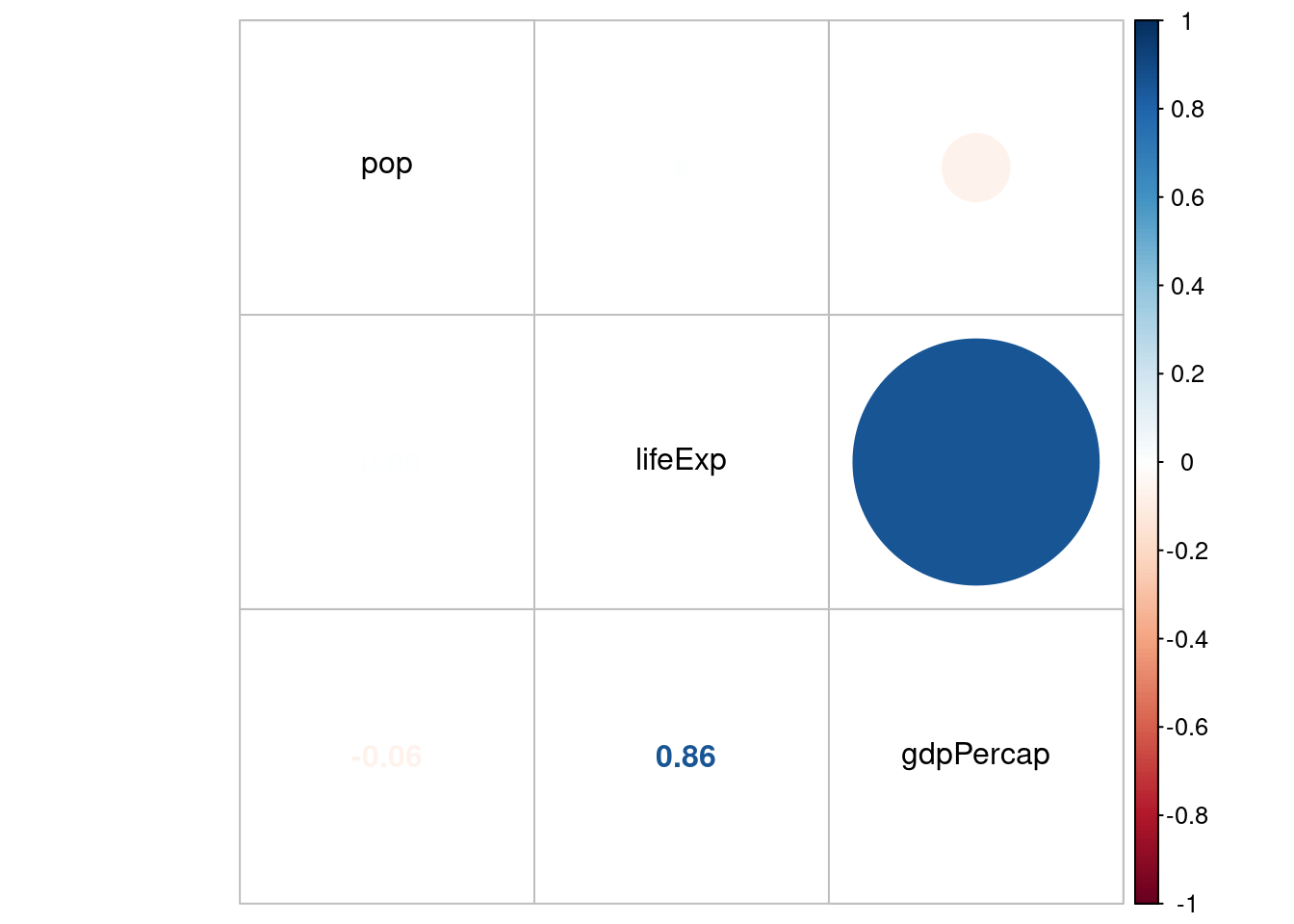
library(RColorBrewer)
corrplot(kor$r, type="upper", order="hclust", col=brewer.pal(n=8, name="RdYlBu"))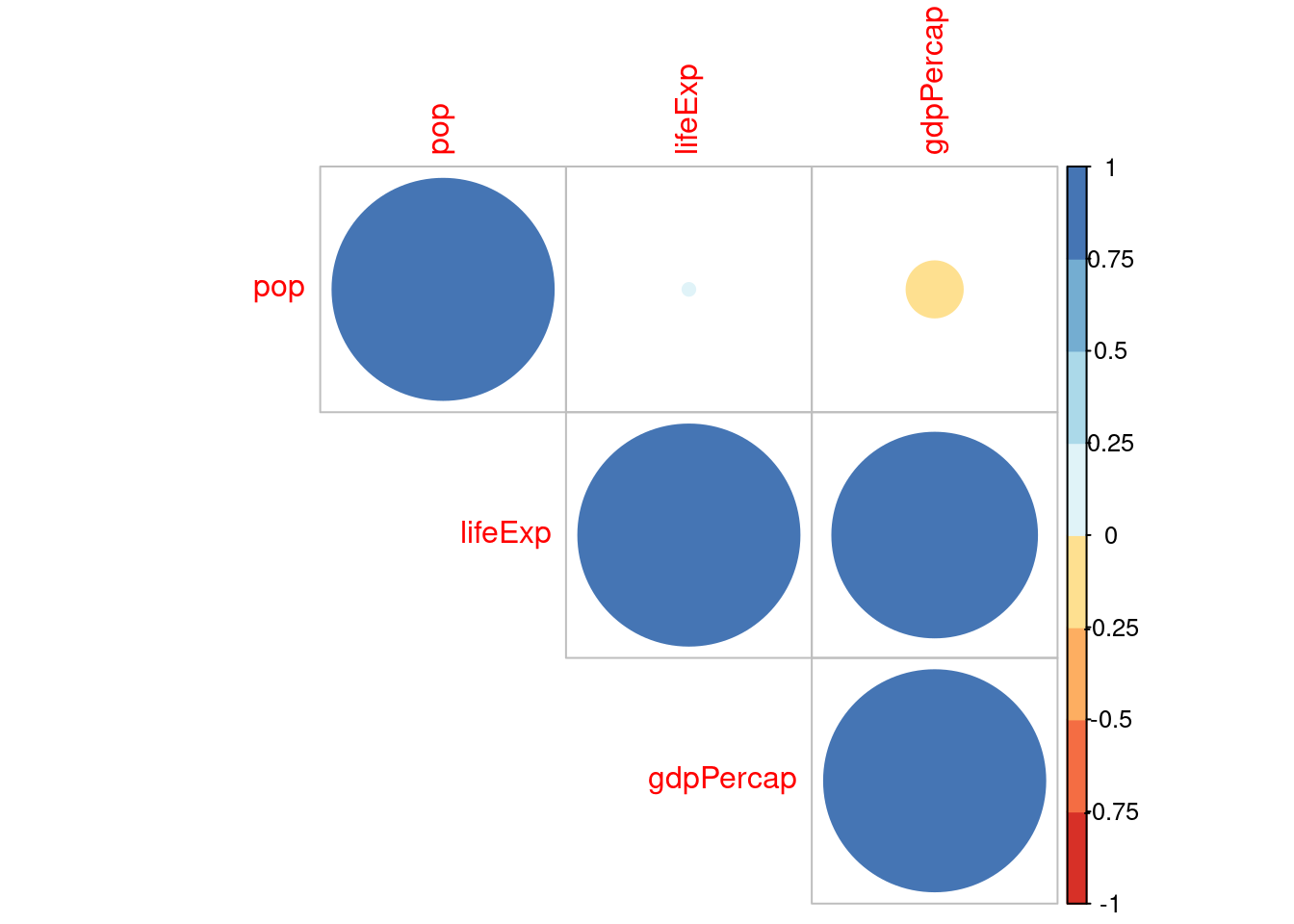
- Funckja
scatterplotMatrix()z pakietucar
library(car)
scatterplotMatrix(~lifeExp+gdpPercap+pop, data=gapminder2007_s)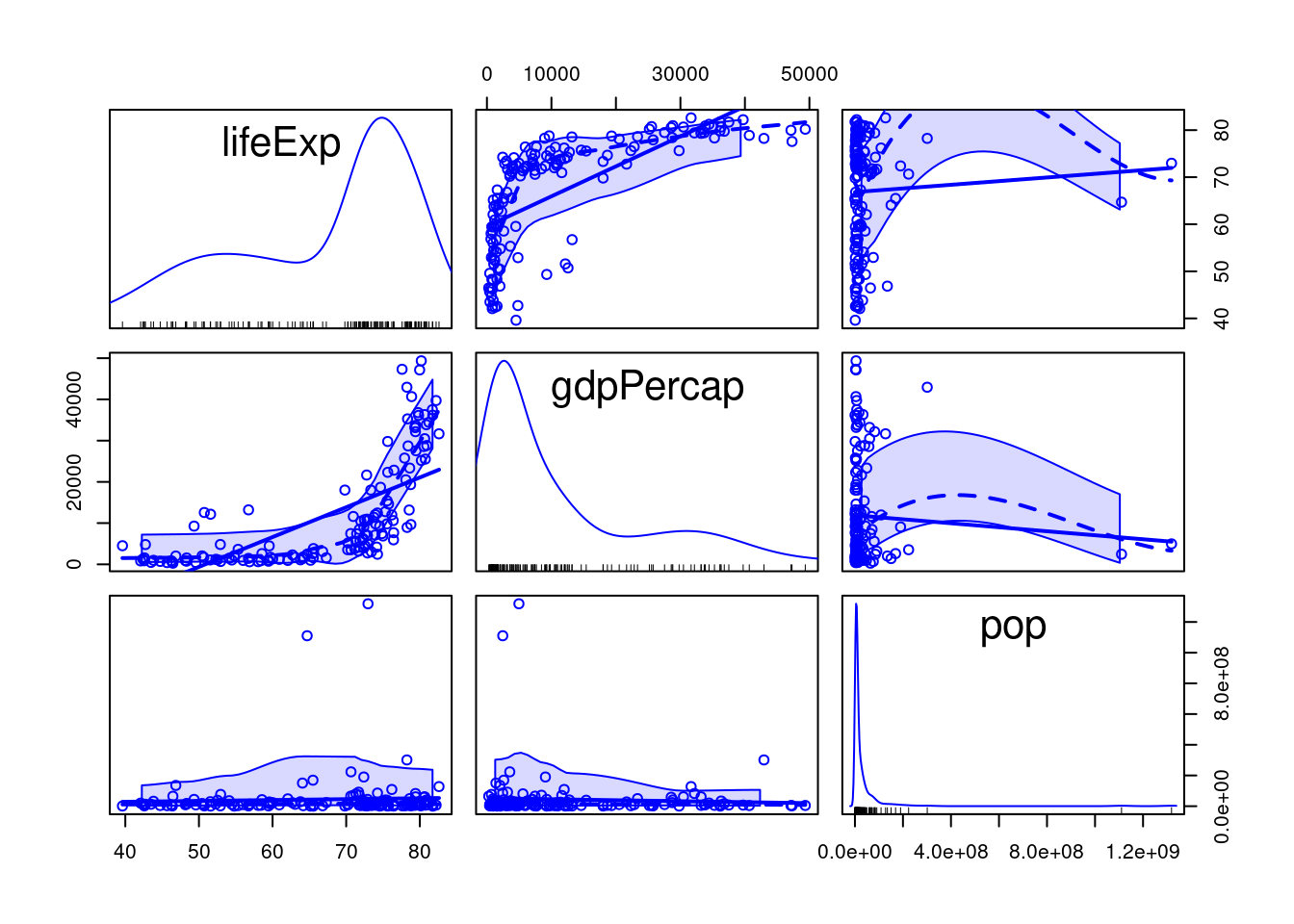
- Funkcja
chart.Correlation()z pakietuPerformanceAnalytics
library(PerformanceAnalytics)
chart.Correlation(gapminder2007_s, histogram=TRUE, pch=19, method = "spearman")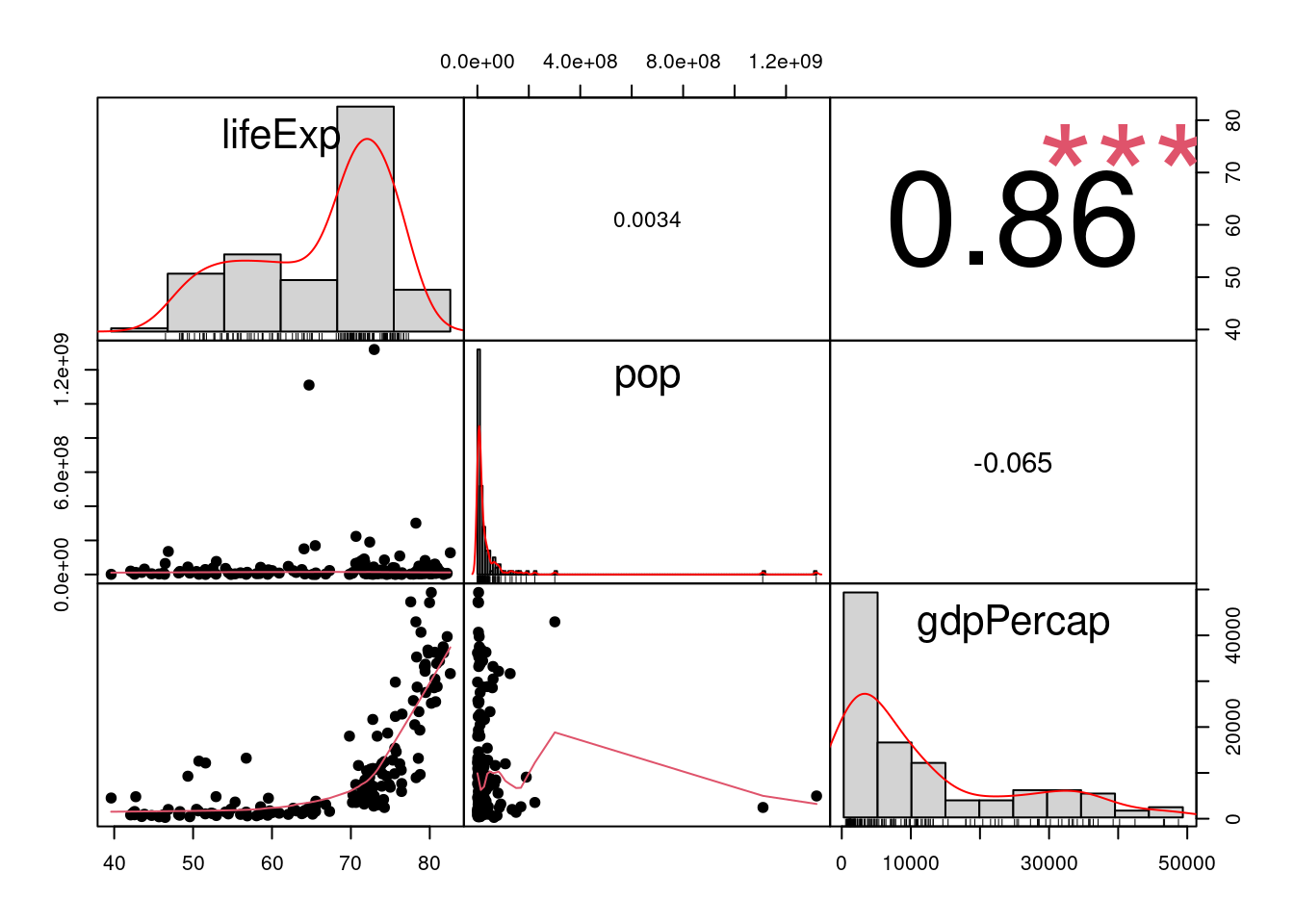
- Funkcja
pairs.panels()z pakietupsych
Współczynnik korelacji (“pearson”, “spearman”) definiowany jest poprzez argument method.
library(psych)
pairs.panels(gapminder2007_s, scale=TRUE, method="spearman")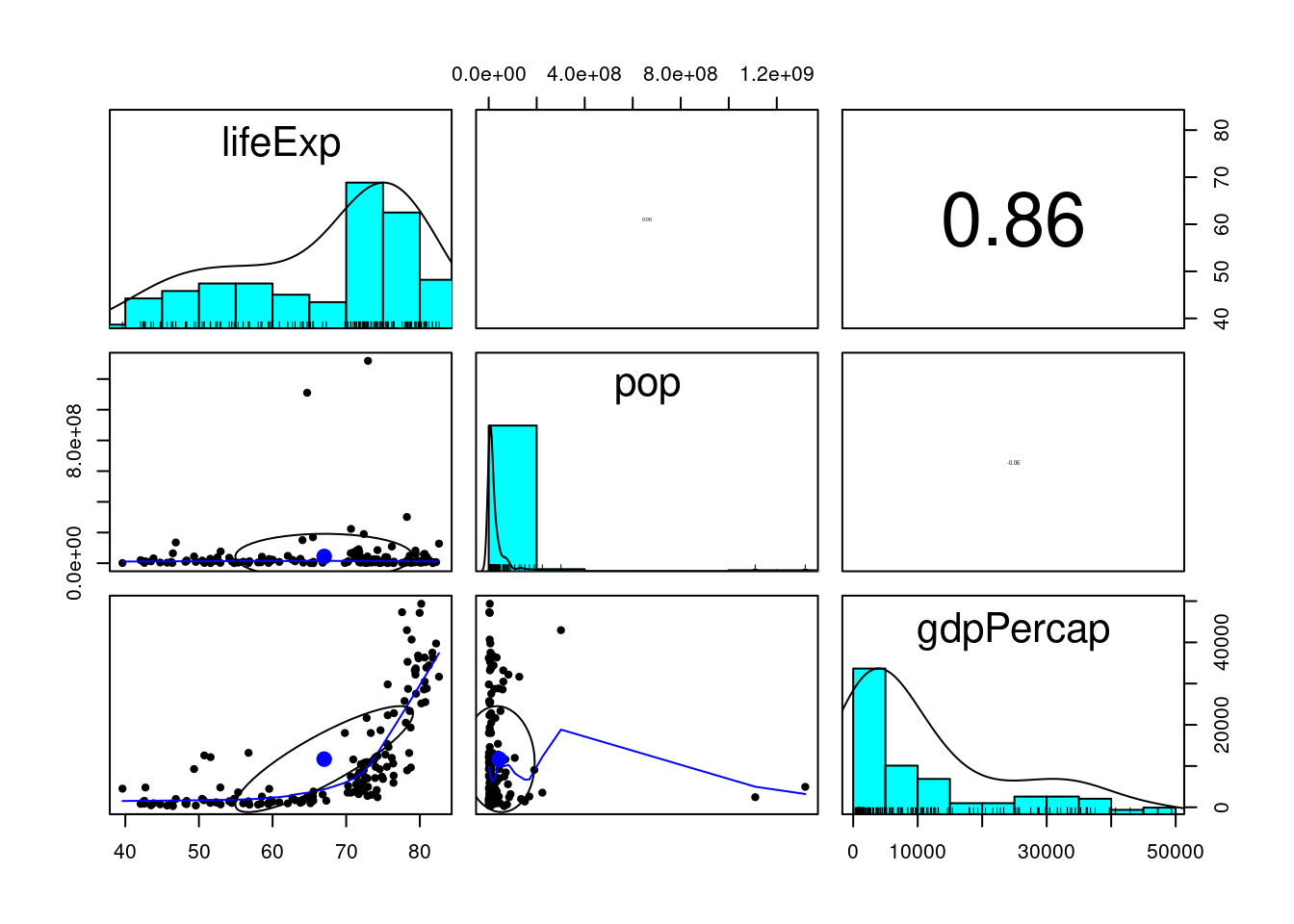
- Funkcja
ggcorr()iggpairs()z pakietuGGally
Argument method składa się z dwóch elementów: pierwszy określa sposób działania przy braku danych (“everything”, “all.obs”, “complete.obs”, “na.or.complete” or “pairwise.complete.obs”), drugi - współczynnik korelacji (“pearson”, “kendall” or “spearman”). Domyślan opcja to c("pairwise", "pearson").
library(GGally)
ggcorr(gapminder2007_s, method = c("pairwise", "spearman"), nbreaks=8, palette='RdGy', label=TRUE, label_size=5, label_color='white')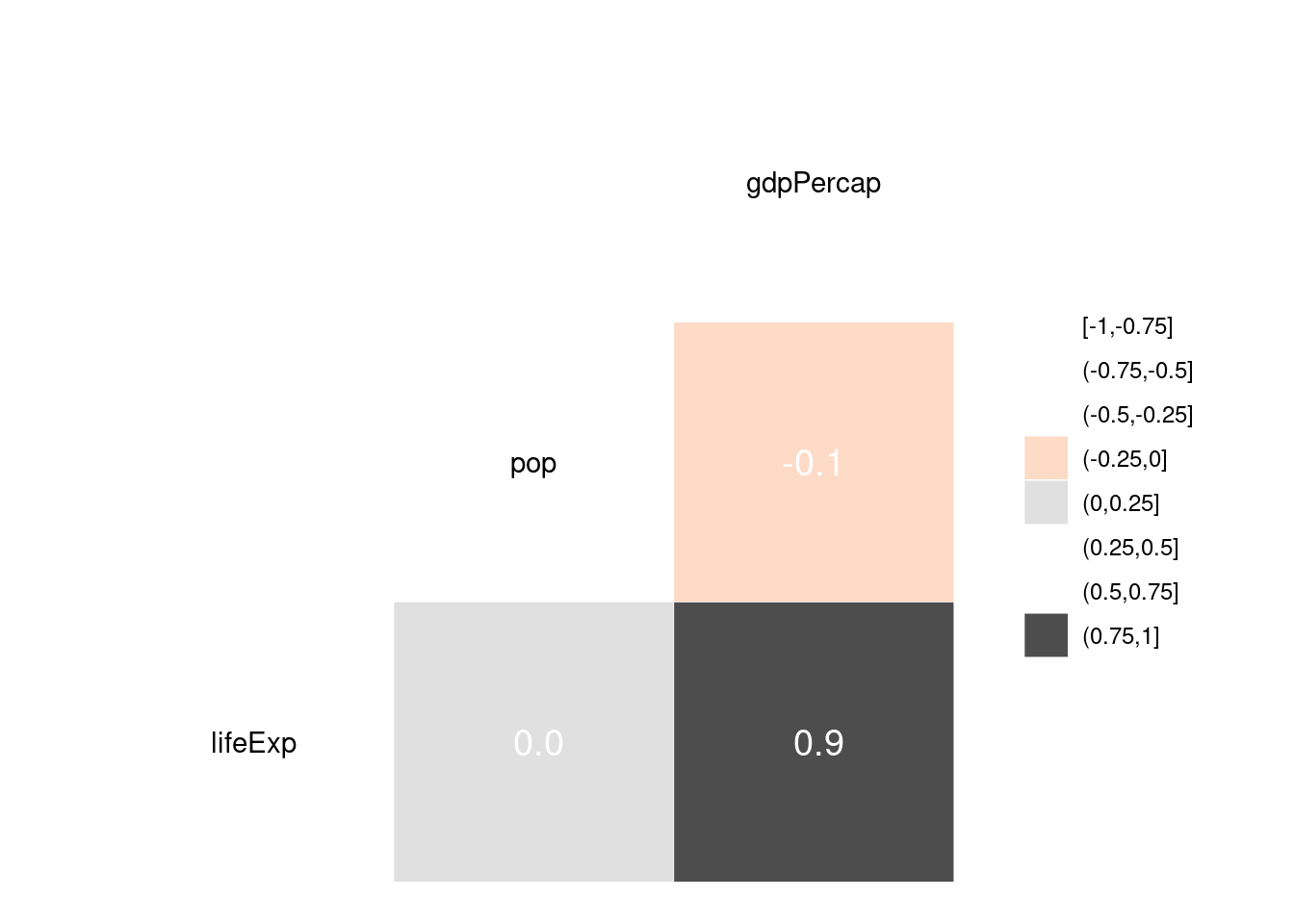
Współczynnik korelacji liniowej Pearsona
library(GGally)
ggpairs(gapminder2007_s) 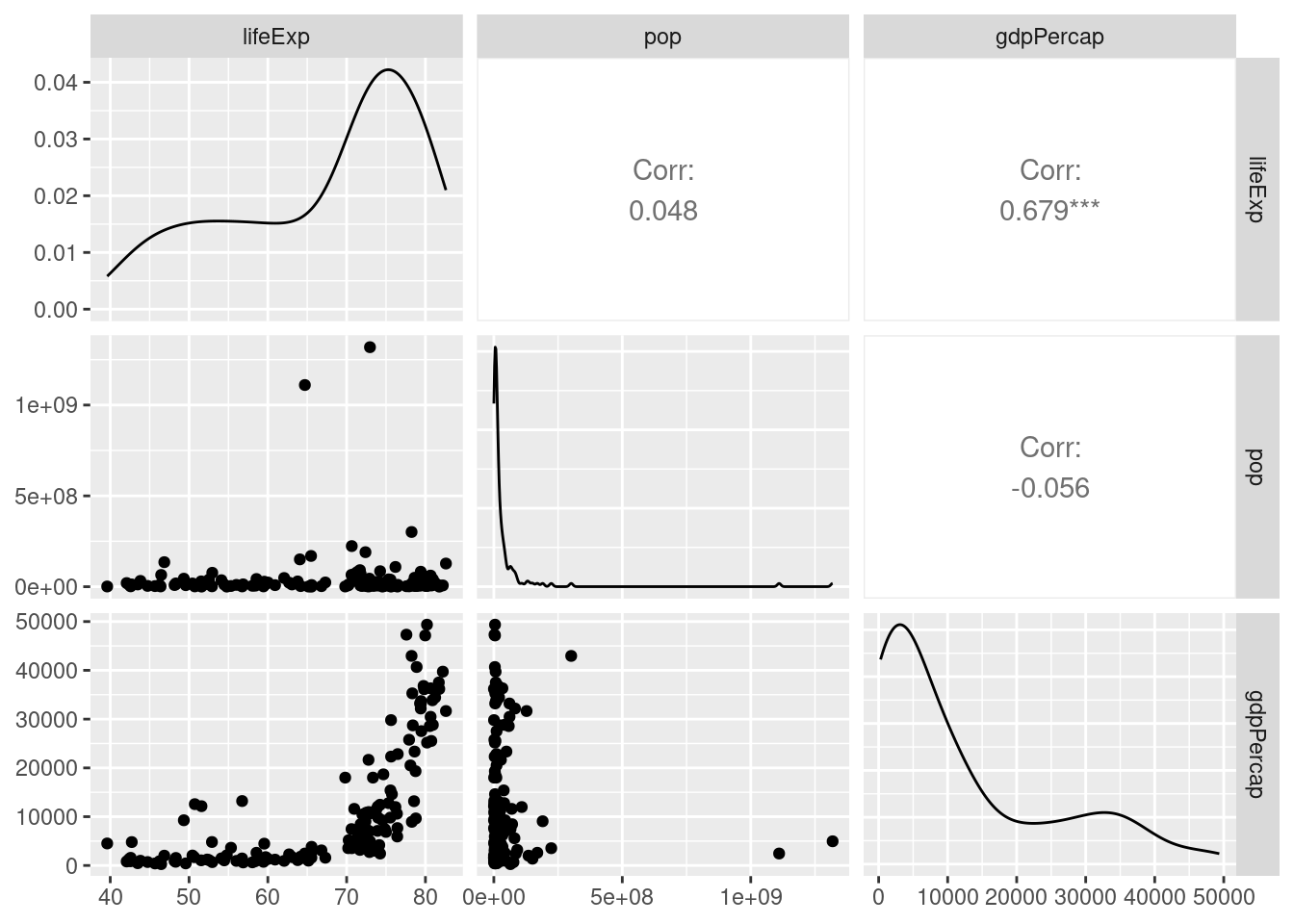
Współczynnik korelacji rang Spearmana
library(GGally)
ggpairs(gapminder2007_s,
upper = list(continuous = wrap(ggally_cor, method = "spearman")))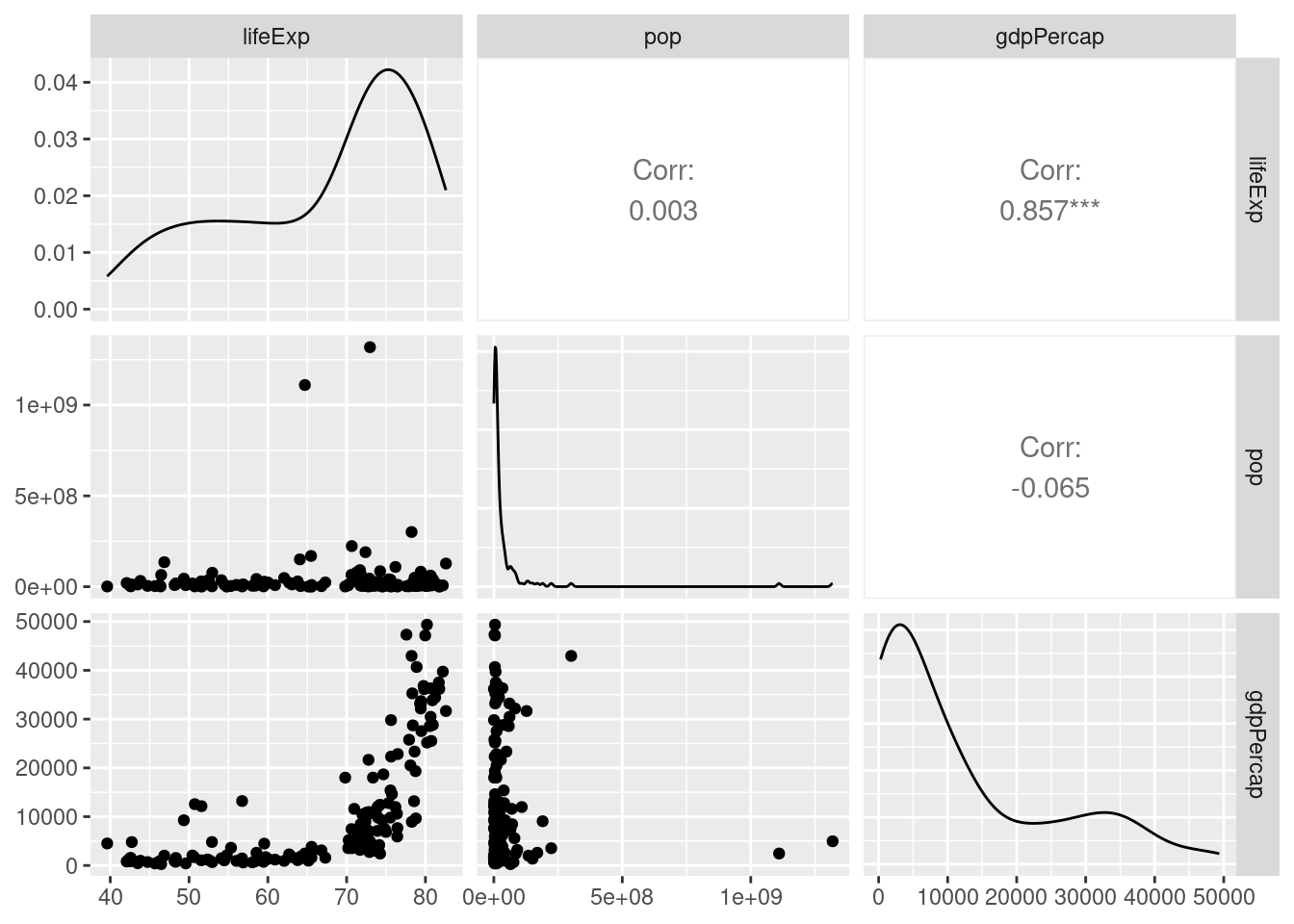
Używając danych
gapminderz pakietu gapminder wyselekcjonuj dane dla roku 1987 oraz zachowaj tylko kolumny lifeExp, gdpPercap, pop. Zwizualizuj w postaci macierzy wykresów rozrzutu relację pomiędzy tymi trzema zmiennymi. Wylicz korelację. Co oznacza wynik?
Rozwiązanie:
Uwaga! W rozwiązaniu wykorzystano funkcję ggpairs z biblioteki GGally. Biblioteka PerformanceAnalytics nie może zostać wykorzystana w interaktywnym edytorze.
gapminder87 <- gapminder %>%
filter(year == 1987) %>%
select(lifeExp, gdpPercap, pop)
library(GGally)
ggpairs(gapminder87,
upper = list(continuous = wrap(ggally_cor, method = "spearman")))