5  Statystyki opisowe

Statystyki opisowe wykorzystuje się do przedstawienia ogólnej charakterystyki danych.

Statystyki opisowe dzielimy na:

1. Miary położenia - określają przeciętny poziom oraz rozmieszczenie wartości zmiennej:

   • Miary przeciętne - np. średnia arytemtyczna - charakteryzują średni lub typowy poziom wartości zmiennej; mówią zatem o przeciętnym poziomie rozważanej zmiennej;
   • Wartość modalna - wartość najczęściej występująca w zbiorze danych;
   • Kwantyle - dzielą zbiorowość na określone części, np. 4, 10, 100 części.

2. Miary rozrzutu - określają granice zmienności danej zmiennej:

   • rozstęp;
   • rozstęp kwartylowy;
   • odchylenie standardowe.

3. Miary asymetrii i koncentracji.

   • skośność;
   • kurtoza.

library(gapminder)
library(dplyr)

data('gapminder', package ='gapminder')
dane2007 <- filter(gapminder, year==2007)

5.1 Podstawowe statystyki

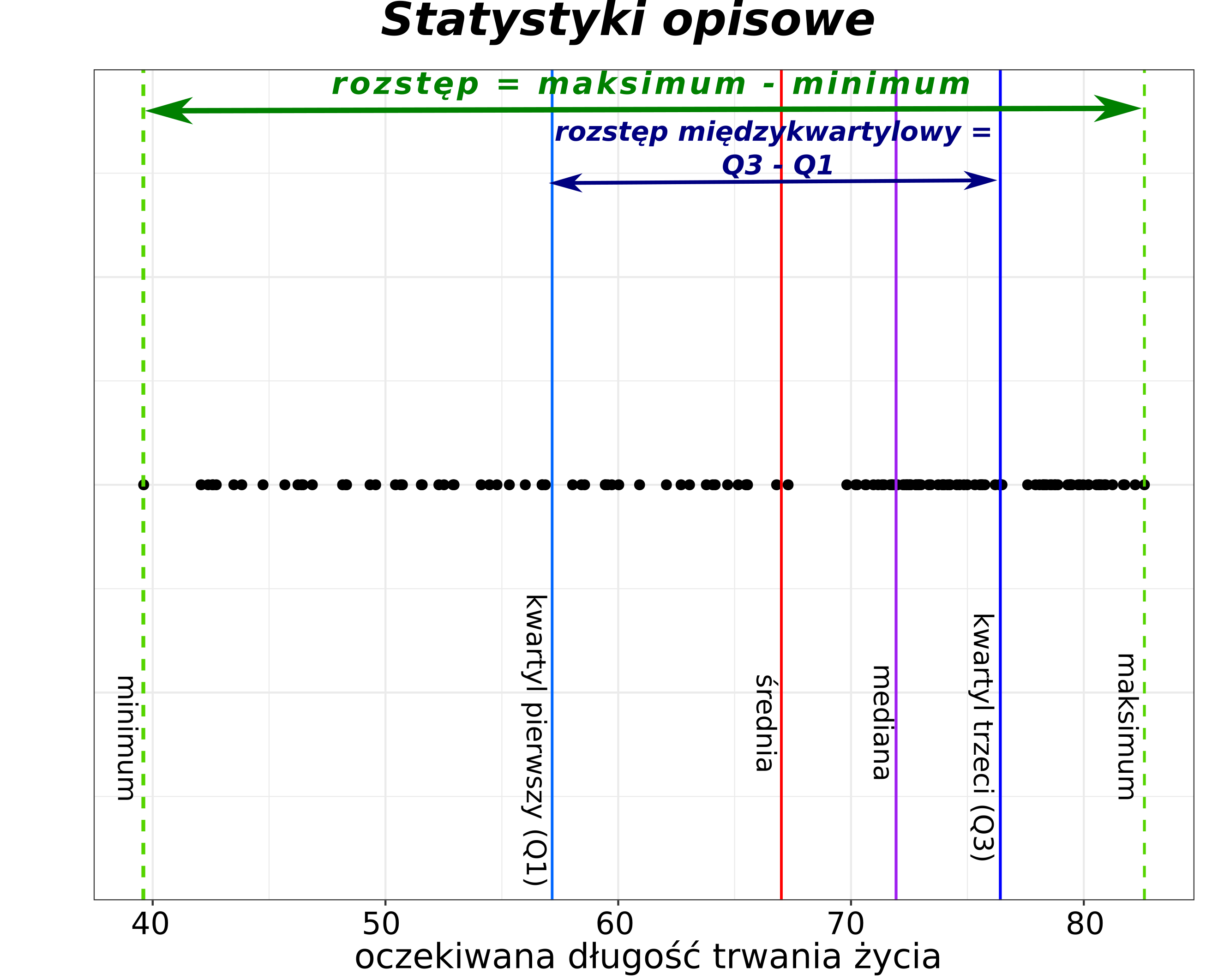
Zestaw podstawowych statystyk opisowych obliczany jest za pomocą funkcji summary(). Funkcja ta oblicza wartość minimalną, wartość maksymalną, pierwszy i trzeci kwartyl, medianę oraz średnią.

summary(dane2007)

        country       continent       year         lifeExp     
 Afghanistan:  1   Africa  :52   Min.   :2007   Min.   :39.61  
 Albania    :  1   Americas:25   1st Qu.:2007   1st Qu.:57.16  
 Algeria    :  1   Asia    :33   Median :2007   Median :71.94  
 Angola     :  1   Europe  :30   Mean   :2007   Mean   :67.01  
 Argentina  :  1   Oceania : 2   3rd Qu.:2007   3rd Qu.:76.41  
 Australia  :  1                 Max.   :2007   Max.   :82.60  
 (Other)    :136                                               
      pop              gdpPercap      
 Min.   :1.996e+05   Min.   :  277.6  
 1st Qu.:4.508e+06   1st Qu.: 1624.8  
 Median :1.052e+07   Median : 6124.4  
 Mean   :4.402e+07   Mean   :11680.1  
 3rd Qu.:3.121e+07   3rd Qu.:18008.8  
 Max.   :1.319e+09   Max.   :49357.2  
                                      

5.2 Statystyki opisowe: Miary położenia

5.2.1 Średnia arytmetyczna

• Obliczana jest jako iloraz sumy liczb i ilości tych liczb.
• Jest najczęściej używaną miarą charakteryzującą rozkład cechy
• Wady: czuła na wartości odstające

srednia_lifeExp <- mean(dane2007$lifeExp)
srednia_lifeExp 

[1] 67.00742

Obliczyć średnią wartość dla PKB (gdpPercap) w 2007 roku.

Solution

Rozwiązanie:

mean(dane2007$gdpPercap)     

Ile wynosiła średnia oczekiwana długość trwania życia w Azji w roku 2002?

Solution

Rozwiązanie:

asia2002 <- filter(gapminder, continent == 'Asia' & year == 2002) 
mean(asia2002$lifeExp)

5.2.2 Średnia ważona

srednia_w_lifeExp <- weighted.mean(dane2007$lifeExp, dane2007$pop)

5.2.3 Średnia harmoniczna

harmonic_mean = function(x){
  1 / mean(1 / x)
}

rzeka = c(6, 3.2) #km/h
harmonic_mean(rzeka)

[1] 4.173913

5.2.4 Średnia geometryczna

geometric_mean = function(x){
  n = length(x)
  prod(x) ^ (1 / n)
}

zmiana <- c(1.026392, 1.011959)
geometric_mean(zmiana)

[1] 1.01915

5.2.5 Kwantyle

Kwantyle to wartości cechy, które dzielą analizowany zbiór danych na określone części pod względem liczby jednostek. Części te pozostają w stosunku do siebie w określonych proporcjach:

• Kwartyle - podział na 4 części:
  • Kwartyl pierwszy (Q1)
  • Mediana - kwartyl drugi
  • Kwartyl trzeci (Q3)
• Decyle - podzial na 10 części
• Percentyle - podział na 100 częsci

Funkcja quantile() oblicza dowolną wartość kwantyli. Argument probs pozwala na zdefyniowanie dowolnych wartości, które mają zostać wyliczone. Argument ten przyjmuje wartości z przedziału od 0 do 1.

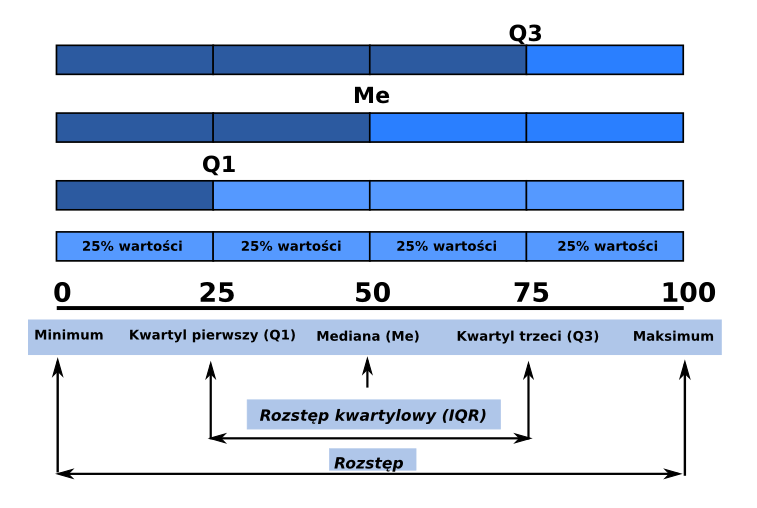
Kwartyle

Funkcja quantile() domyślnie zwraca wartośći kwartyli.

kwartyle <- quantile(dane2007$lifeExp)
kwartyle

      0%      25%      50%      75%     100% 
39.61300 57.16025 71.93550 76.41325 82.60300 

Kwartyle są także obliczane przez funkcję summary(), która dodatkowo zwraca także wartości minimalną, maksymalną oraz średnią.

Decyle

W poniższym przykładzie seq(0,1,0.1) zwraca sekwencję wartości od 0 do 1 z krokiem co 0.1. Odpowiada to podziałowi danych na 10 równych części.

decyle <- quantile(dane2007$lifeExp, probs = seq(0, 1, 0.1))
decyle

     0%     10%     20%     30%     40%     50%     60%     70%     80%     90% 
39.6130 48.1734 54.1814 59.8127 67.0006 71.9355 73.2048 75.4719 78.2668 79.8223 
   100% 
82.6030 

Percentyle

W poniższym przykładzie zbiór zostanie podzielony na 100 równych części.

percentyle <- quantile(dane2007$lifeExp, probs = seq(0, 1, 0.01))
head(percentyle, 10)

      0%       1%       2%       3%       4%       5%       6%       7% 
39.61300 42.20582 42.53488 42.62397 43.21484 43.87365 45.17202 46.16868 
      8%       9% 
46.40872 46.73593 

Dowolne wartości kwantyli

W poniższym przykładzie zostanie wyliczony 5 oraz 95 percentyl.

q <- quantile(dane2007$lifeExp, probs = c(0.05, 0.95))
q

      5%      95% 
43.87365 80.74060 

Obliczyć decyle dla gdpPercap dla danych z 2007 roku.

Solution

Rozwiązanie:

quantile(dane2007$gdpPercap, probs = seq(0, 1, 0.1))

Obliczyć pierwszy i trzeci kwartyl dla oczekiwanej długości trwania życia w Afryce w 2002 roku.

Solution

Rozwiązanie:

africa2002 <- filter(gapminder, continent == 'Africa' & year == 2002)
quantile(africa2002$lifeExp, probs = c(0.25, 0.75))

Mediana

Mediana to wartość, która dzieli zbiór danych na 2 równe części. Mediana obliczana jest przez funkcję median().

median_lifeExp <- median(dane2007$lifeExp)
median_lifeExp 

[1] 71.9355

Obliczyć medianę dla gdpPercap dla danych z 2007 roku.

Solution

Rozwiązanie:

median(dane2007$gdpPercap)    

Ile wynosiła mediana oczekiwanej długości trwania życia w Afryce w 1952 roku?

Solution

Rozwiązanie:

africa1952 <- filter(gapminder, continent == 'Africa' & year == 1952)
median(africa1952$lifeExp) 

Mediana a średnia arytmetyczna

• dla rozkładu symetrycznego mediana oraz średnia będą równe.
• mediana jest lepszą miarą w przypadku rozkładów skośnych.
• średnia jest bardziej czuła na wartości odstające.
• średnia jest bardziej przydatna dla małych zbiorów danych.

Podsumowanie: Warto podawać obie wartości.

5.2.6 Wartość modalna

• wartość cechy, która w zbiorze danych występuje najczęściej. W R nie ma wbudowanej funkcji do obliczania tej statystyki.

5.3 Statystyki opisowe: Miary rozrzutu

5.3.1 Minimum i maksimum

min_lifeExp <- min(dane2007$lifeExp)
min_lifeExp

[1] 39.613

max_lifeExp <- max(dane2007$lifeExp)
max_lifeExp

[1] 82.603

range(dane2007$lifeExp)

[1] 39.613 82.603

Ile wynosiła najmniejsza i największa oczekiwana długość trwania życia w Afryce w roku 1952?

Solution

Rozwiązanie:

africa1952 <- filter(gapminder, continent == 'Africa' & year == 1952)
range(africa1952$lifeExp)

Oblicz zakres oczekiwanej długości trwania życia w Polsce w latach 1952-2007?

Solution

Rozwiązanie:

# Rozwiazanie 1
pl <- filter(gapminder, country == 'Poland')
range(pl$lifeExp)

# Rozwiazanie 2 
min(pl$lifeExp)
max(pl$lifeExp)

W jakim zakresie zmieniała się oczekiwana długość trwania życia w 2002 roku w krajach azjatyckich z PKB (gpdPercap) przekraczającym 25000?

Solution

Rozwiązanie:

asia2002 <- filter(gapminder, year == 2002 & continent == 'Asia' & gdpPercap > 25000)
range(asia2002$lifeExp)

5.3.2 Rozstęp

• najprostsza miara zmienności
• różnica między wartości maksymalną oraz wartością minimalną
• wrażliwy na wartości odstające

range_lifeExp <- max(dane2007$lifeExp) - min(dane2007$lifeExp)

Uwaga! W R funkcja range() zwraca wektor składający się z dwóch wartości - minimalnej oraz maksymalnej, a nie rostęp (różnicę między tymi wartościami).

Obliczyć rozstęp dla gdpPercap dla danych z 2007 roku.

Solution

Rozwiązanie:

 max(dane2007$gdpPercap) - min(dane2007$gdpPercap)

5.3.3 Rozstęp kwartylowy

• różnica między kwartylem trzecim i kwartylem pierwszym

IQR_lifeExp <- IQR(dane2007$lifeExp)

Obliczyć rozstęp kwartylowy dla gdpPercap dla danych z 2007 roku.

Solution

Rozwiązanie:

IQR(dane2007$gdpPercap)   

Obliczyć rozstęp kwartylowy dla oczekiwanej długości trwania życia w Afryce

Solution

Rozwiązanie:

africa <- filter(gapminder, continent == 'Africa')  
IQR(africa$lifeExp)

5.3.4 Wariancja

• wariancja oraz odchylenie standardowe mierzą jak daleko dane rozchodzą się od średniej.

var_lifeExp <- var(dane2007$lifeExp)

5.3.5 Odchylenie standardowe

• obliczane jako pierwiastek z wariancji

• obok średniej jest jednym z najczęściej stosowanych parametrów statystycznych:

  • jest obliczane ze wszystkich obserwacji w zbiorze danych
  • im zbiór danych jest bardziej zróżnicowany tym większe odchylenie standardowe.

• małe odchylenie standardowe - wartości są blisko średniej

• duże odchylenie standardowe - wartości są daleko od średniej.

sd_lifeExp <- sd(dane2007$lifeExp)
sd_lifeExp 

[1] 12.07302

Jakie była wartość odchylenia standardowego dla gdpPercap w 2007 roku?

Solution

Rozwiązanie:

sd(dane2007$gdpPercap)

5.4 Opisywanie danych nominalnych

5.4.1 Częstość

table(dane2007$continent)

  Africa Americas     Asia   Europe  Oceania 
      52       25       33       30        2 

table(dane2007$continent) / length(dane2007$continent) * 100

   Africa  Americas      Asia    Europe   Oceania 
36.619718 17.605634 23.239437 21.126761  1.408451 

Ile krajów było w 1952 roku na poszczególnych kontynentach?

Solution

Rozwiązanie:

dane1952 <- filter(gapminder, year == 1952)
table(dane1952$continent)

5.5 Statystykiw grupach

Pakiet dplyr pozwala także na obliczenie statystyk według grup, np. średnia długość trwania życia na poszczególnych kontynentach.

• Średnia oczekiwana długość życia w 2007 roku według kontynentów.

Obliczenie statystyk w grupach wymaga najpierw pogrupowania danych (funkcja group_by()).

gapminder2007 <- filter(gapminder, year == 2007)
by_continent <- group_by(gapminder2007, continent)
smr_by_continent <- summarize(by_continent,
                              mean_le = mean(lifeExp))

smr_by_continent

# A tibble: 5 × 2
  continent mean_le
  <fct>       <dbl>
1 Africa       54.8
2 Americas     73.6
3 Asia         70.7
4 Europe       77.6
5 Oceania      80.7

Powyższy kod można zapisać także z wykorzystaniem operatora łączącego %>%

mean_by_continent <- gapminder %>% 
  filter(year == 2007) %>% 
  group_by(continent) %>% 
  summarize(mean_le = mean(lifeExp))

mean_by_continent

# A tibble: 5 × 2
  continent mean_le
  <fct>       <dbl>
1 Africa       54.8
2 Americas     73.6
3 Asia         70.7
4 Europe       77.6
5 Oceania      80.7

Oblicz średnią oczekiwaną długość trwania życia w poszczególnych latach. Posortuj wyniki od największej do najmniejszej wartości.

Solution

Rozwiązanie:

ex15 <- gapminder %>% 
  group_by(year) %>% 
  summarize(mean_le = mean(lifeExp)) %>% 
  arrange(desc(mean_le))
ex15

Jak zmieniało się w poszczególnych latach średnie PKB w Afryce?

Solution

Rozwiązanie:

ex16  <- gapminder %>% 
  filter(continent == 'Africa')  %>% 
  group_by(year) %>% 
  summarize(mean_gpd = mean(gdpPercap))  
ex16

• Średnia oczekiwana długość życia w podziale na kontynenty oraz lata.

by_continent_year <- group_by(gapminder, continent, year)
smr_by_continent_year <- summarize(by_continent_year,
                              mean_le = mean(lifeExp))

`summarise()` has grouped output by 'continent'. You can override using the
`.groups` argument.

smr_by_continent_year

# A tibble: 60 × 3
# Groups:   continent [5]
   continent  year mean_le
   <fct>     <int>   <dbl>
 1 Africa     1952    39.1
 2 Africa     1957    41.3
 3 Africa     1962    43.3
 4 Africa     1967    45.3
 5 Africa     1972    47.5
 6 Africa     1977    49.6
 7 Africa     1982    51.6
 8 Africa     1987    53.3
 9 Africa     1992    53.6
10 Africa     1997    53.6
# ℹ 50 more rows

Oblicz średnią wartość gdpPercap w 2007 roku w podziale na kontynenty.

Solution

Rozwiązanie:

ex17 <- gapminder %>% 
  filter(year == 2007) %>% 
  group_by(continent) %>% 
  summarize(mean_gpd = mean(gdpPercap))  
  
ex17

Oblicz średnią wartość gdpPercap w podziale na poszczególne kontynenty oraz lata. Przedstaw wynik w “układzie szerokim” - każdy wiersz to określony kontynent, a każda kolumna to określony rok.

Solution

Rozwiązanie:

ex18 <- gapminder %>% 
 group_by(continent, year) %>% 
 summarize(mean_gdp = mean(gdpPercap)) %>% 
 pivot_wider(names_from = year, values_from = mean_gdp)
ex18

5.6 Braki danych

W R braki danych zazwyczaj kodowane są jako NA - Not Available.

NA + 1 

[1] NA

2*NA 

[1] NA

x = c(1,2,NA)
mean(x)

[1] NA

mean(x, na.rm = TRUE)

[1] 1.5

5.7 Ćwiczenie

Wykorzystując zbiór danych gapminder sformułuj dwa pytania i odpowiedz na nie.