14 Testy parametryczne
14.1 Testy t-Studenta
Służą do wnioskowania o wartości średniej w populacji, z której pobraliśmy próbę losową.
Służą do porównania ze sobą dwóch grup
Można wyróżnić trzy rodzaje testów t-Studenta:
- dla prób niezależnych
- dla prób zależnych
- dla jednej próby
Założenia testów t-Studenta
- Rozkład danych obserwacji jest zbliżony do rozkładu normalnego
- Badane grupy mają zbliżoną liczebność
- Wartości w badanych grupach wykazują podobną wariancję (homogeniczność wariancji)
- Zmienne powinny być ilościowe
Hipoteza statystyczna
Hipoteza zerowa: \(H_0 : \mu_1 = \mu_2\)
Hipotezy alternatywne:
- test jednostronny: \(H_A : \mu_1 > \mu_2\)
- test dwustronny: \(H_A : \mu_1 \neq \mu_2\)
14.1.1 Test t-Studenta dla prób niezależnych
- Dotyczy porównania ze sobą dwóch różnych grup obserwacji
- Próby muszą być od siebie niezależne (wyniki pomiaru jednej grupy nie zależą od wyników pomiaru drugiej grupy)
Przykład: Czy istnieją istotne różnice w średniej temperaturze (annual_tavg) między Niżem Wschodniobałtycko-Białoruskim, a Wyżynami Polskimi?
library(dplyr)
Attaching package: 'dplyr'The following objects are masked from 'package:stats':
filter, lagThe following objects are masked from 'package:base':
intersect, setdiff, setequal, unionpomiary_pol = read.csv("data/pomiary_pol.csv")
pomiary_pol2 = filter(pomiary_pol,
prowincja %in%
c("Niż Wschodniobałtycko-Białoruski",
"Wyżyny Polskie"))
head(pomiary_pol2) pomiar_id tmin_4 tmax_4 tmin_9 tmax_9 annual_tavg annual_precip
1 2 4.122184 14.35588 9.214639 19.32696 8.144152 644.7503
2 8 2.656403 12.32077 8.042327 17.45611 6.614168 625.5083
3 20 3.528041 13.42039 8.415737 18.41839 7.387148 544.4395
4 22 3.636560 13.50256 8.553030 18.40303 7.309585 562.4307
5 24 4.297906 14.19705 9.064549 18.89787 7.654198 539.5709
6 29 2.769288 12.26086 8.207968 17.51594 6.660865 591.5201
prow_id woj_id prowincja wojewodztwo
1 6 13 Wyżyny Polskie świętokrzyskie
2 6 9 Wyżyny Polskie podkarpackie
3 6 3 Wyżyny Polskie lubelskie
4 6 3 Wyżyny Polskie lubelskie
5 6 3 Wyżyny Polskie lubelskie
6 5 10 Niż Wschodniobałtycko-Białoruski podlaskielibrary(ggplot2)
ggplot(pomiary_pol2, aes(x = prowincja, y = annual_tavg)) +
geom_boxplot() +
labs(x = "Prowincja", y = "Temperatura powietrza [C]") +
theme_bw()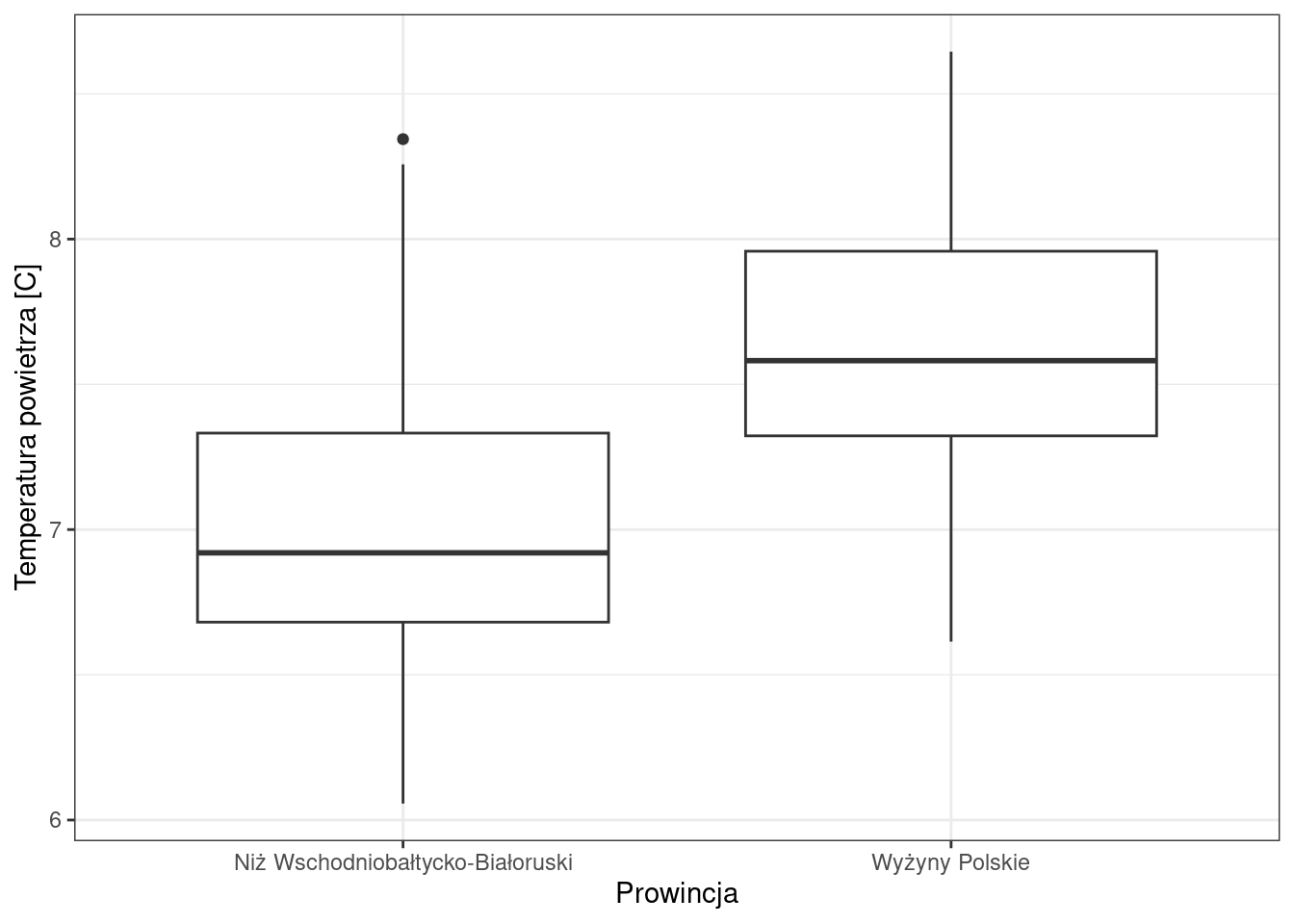
Testowanie istotności różnic przy założeniu hipotezy dwustronnej tj. \(\mu_{Niż} \neq \mu_{Wyżyny}\)
t.test(annual_tavg ~ prowincja, data = pomiary_pol2)
Welch Two Sample t-test
data: annual_tavg by prowincja
t = -13.475, df = 338.76, p-value < 2.2e-16
alternative hypothesis: true difference in means between group Niż Wschodniobałtycko-Białoruski and group Wyżyny Polskie is not equal to 0
95 percent confidence interval:
-0.7378497 -0.5498738
sample estimates:
mean in group Niż Wschodniobałtycko-Białoruski
6.979376
mean in group Wyżyny Polskie
7.623238 Intepretacja wyników
Poziom prawdopodobieństwa p (p-wartość) - jest to wyliczany w pakietach komputerowych najmniejszy poziom istotności, przy której wyliczona wartość testującej statystyki doprowadza do odrzucenia hipotezy zerowej.
Jeśli p-wartość jest poniżej założonego poziomu istotności (np. 0.05) tzn. że hipotezę zerową możemy odrzucić na rzecz hipotezy alternatywnej.
W powyższym przykładzie:
Hipoteza zerowa: prawdziwa różnica w średnich jest równa 0
Hipoteza alternatywna: Prawdziwa róznica w średnich nie jest równa 0.
P-wartość < 2.2e-16
- P-wartość jest mniejsza od 0.05 a zatem możemy odrzucić hipotezę zerową (różnica w średnich równa 0) na rzecz hipotezy alternatywnej (różnica w średnich różna od 0)
Pytanie: Czy średnia temperatura powietrza na Niżu i na Wyżynach różni się istotnie?
Odpowiedź: Średnia temperatura na Niżu i na Wyżynach różni się istotnie.
Przykład: Czy średnia temperatura (annual_tavg) Niżu Wschodniobałtycko-Białoruskiego jest istotnie wyższa od tempratury na Wyżynach Polskich?
Testowanie istotności różnic przy założeniu hipotezy jednostronnej tj. \(\mu_{Niż} > \mu_{Wyżyny}\)
t.test(annual_tavg ~ prowincja, data = pomiary_pol2,
alternative = "greater")
Welch Two Sample t-test
data: annual_tavg by prowincja
t = -13.475, df = 338.76, p-value = 1
alternative hypothesis: true difference in means between group Niż Wschodniobałtycko-Białoruski and group Wyżyny Polskie is greater than 0
95 percent confidence interval:
-0.7226726 Inf
sample estimates:
mean in group Niż Wschodniobałtycko-Białoruski
6.979376
mean in group Wyżyny Polskie
7.623238 Jaka jest interpretacja powyższego wyniku testu?
Przykład: Czy średnia temperatura (annual_tavg) Niżu Wschodniobałtycko-Białoruskiego jest istotnie niższa od tempratury na Wyżynach Polskich?
Testowanie istotności różnic przy założeniu hipotezy jednostronnej tj. \(\mu_{Niż} < \mu_{Wyżyny}\)
t.test(annual_tavg ~ prowincja, data = pomiary_pol2,
alternative = "less")
Welch Two Sample t-test
data: annual_tavg by prowincja
t = -13.475, df = 338.76, p-value < 2.2e-16
alternative hypothesis: true difference in means between group Niż Wschodniobałtycko-Białoruski and group Wyżyny Polskie is less than 0
95 percent confidence interval:
-Inf -0.5650509
sample estimates:
mean in group Niż Wschodniobałtycko-Białoruski
6.979376
mean in group Wyżyny Polskie
7.623238 Jaka jest interpretacja powyższego wyniku testu?
Wczytaj dane z pliku data/pomiary_pol.csv. Sprawdź czy średnia temperatura roczna (annual_tavg) na Wyżynach Polskich różni się od Masywu Czeskiego? Stwórz wykres porównujący tą zmienną dla tych prowincji. Określ czy różnica pomiędzy średnimi jest istotna statystycznie.
Rozwiązanie:
pomiary_pol = read.csv("data/pomiary_pol.csv")
pomiary_pol2 = filter(pomiary_pol, prowincja %in% c("Masyw Czeski", "Wyżyny Polskie"))
ggplot(pomiary_pol2, aes(x = prowincja, y = annual_tavg)) +
geom_boxplot() +
labs(x = "Prowincja", y = "Temperatura powietrza [C]") +
theme_bw()
t.test(annual_tavg ~ prowincja, data = pomiary_pol2)Wczytaj dane z pliku data/pomiary_pol.csv. Sprawdź czy średnia temperatura roczna (annual_tavg) Masywu Czeskiego jest większa od temperatury na Wyżynach Polskich?
Rozwiązanie:
pomiary_pol = read.csv("data/pomiary_pol.csv")
pomiary_pol2 = filter(pomiary_pol, prowincja %in% c("Masyw Czeski", "Wyżyny Polskie"))
ggplot(pomiary_pol2, aes(x = prowincja, y = annual_tavg)) +
geom_boxplot() +
labs(x = "Prowincja", y = "Temperatura powietrza [C]") +
theme_bw()
t.test(annual_tavg ~ prowincja, data = pomiary_pol2,
alternative = "greater")14.1.2 Test t-Studenta dla prób zależnych
- Dotyczy porównania ze sobą tej samej grupy obserwacji
- Próby są zależne, czyli wynik pomiary w drugim badaniu zależy od pierwszego (dotyczy tej samej obserwacji)
- Służy określeniu wielkości zmian pomiędzy pomiarami
library(dplyr)
library(tidyr)
library(ggplot2)
pomiary_pol = read.csv("data/pomiary_pol.csv")
head(pomiary_pol) pomiar_id tmin_4 tmax_4 tmin_9 tmax_9 annual_tavg annual_precip
1 1 1.796358 12.04034 6.947685 17.84769 6.533702 864.6408
2 2 4.122184 14.35588 9.214639 19.32696 8.144152 644.7503
3 3 3.750375 12.58249 9.513398 17.76400 7.831449 613.0326
4 4 3.645718 12.19533 9.743287 17.69533 7.851240 638.0846
5 5 2.788949 12.58895 7.988949 17.78588 7.296935 546.1904
6 6 4.129882 14.12988 9.300000 19.10000 8.200000 555.2842
prow_id woj_id prowincja
1 2 6 Karpaty Zachodnie z Podkarpaciem Zachodnim i Północnym
2 6 13 Wyżyny Polskie
3 4 16 Niż Środkowoeuropejski
4 4 16 Niż Środkowoeuropejski
5 4 3 Niż Środkowoeuropejski
6 2 9 Karpaty Zachodnie z Podkarpaciem Zachodnim i Północnym
wojewodztwo
1 małopolskie
2 świętokrzyskie
3 zachodniopomorskie
4 zachodniopomorskie
5 lubelskie
6 podkarpackiePrzykład: Czy maksymalna temperatura kwietnia (tmax_4) oraz września (tmax_9) różni się istotnie?
#Wykonanie wykresu pudelkowego wymaga zamiany danych na format dlugi
pomiary_pol_l <- pomiary_pol %>%
select(pomiar_id, tmax_4, tmax_9) %>%
pivot_longer(contains("tmax"))
ggplot(pomiary_pol_l, aes(name, value)) +
geom_boxplot() +
labs(y = "Temperatura powietrza [C]") +
theme_bw()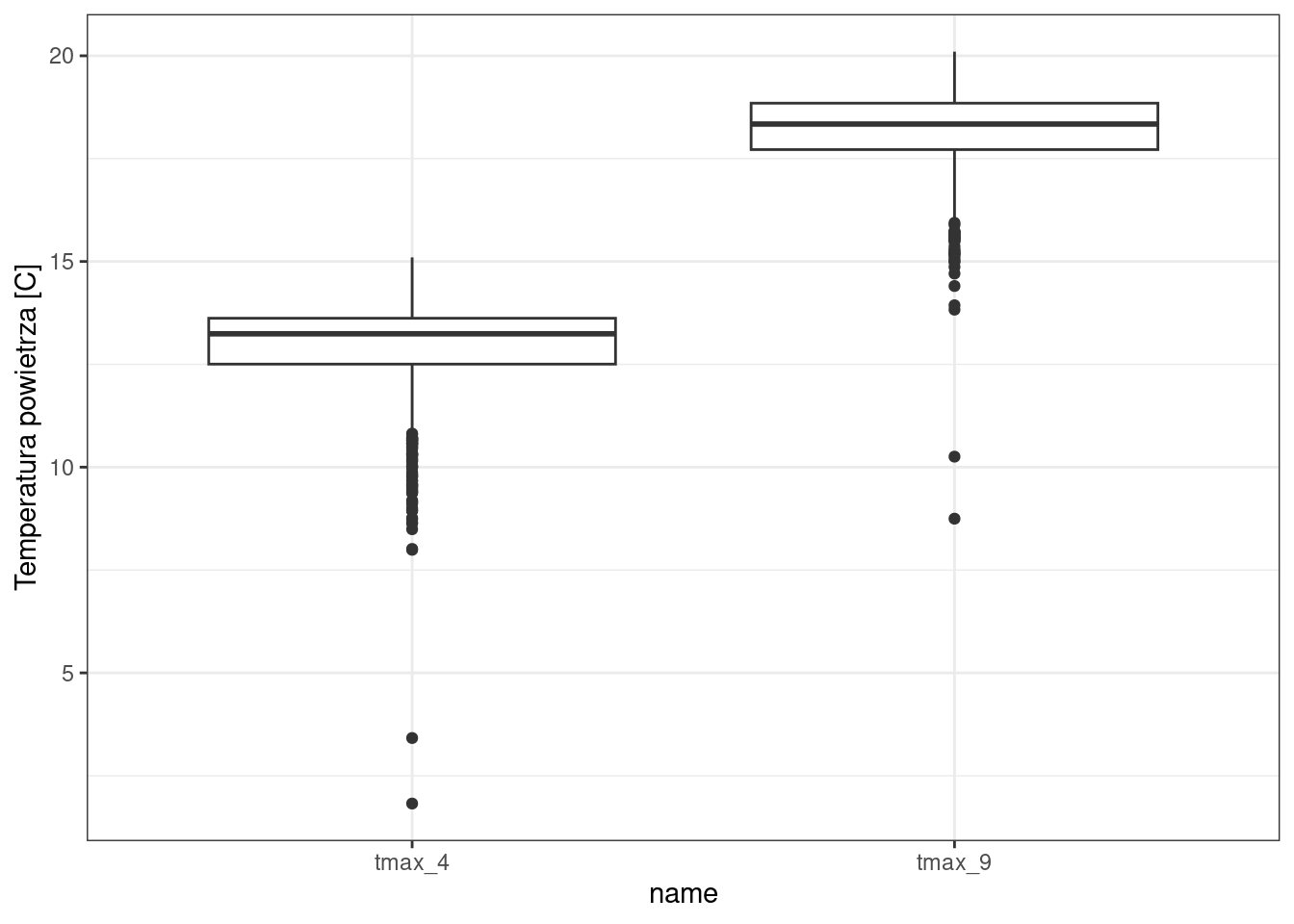
Test t-Studenta dla prób zależnych, jeśli dane są w formacie szerokim.
t.test(pomiary_pol$tmax_4, pomiary_pol$tmax_9, paired = TRUE, alternative = "greater")
Paired t-test
data: pomiary_pol$tmax_4 and pomiary_pol$tmax_9
t = -528.83, df = 1494, p-value = 1
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
-5.26396 Inf
sample estimates:
mean difference
-5.247628 Jaka jest interpretacja powyższego wyniku?
Wczytaj dane z pliku data/pomiary_pol.csv. Wykonaj test dla określenia czy maksymalna temperatura powietrza w kwietniu (tmax_4) jest niższa od maksymalnej temperatury września (tmax_9). Sformułuj hipotezę zerową oraz hipotezę alternatywną oraz zinterpretuj wynik testu.
Rozwiązanie:
pomiary_pol = read.csv("data/pomiary_pol.csv")
t.test(pomiary_pol$tmax_4, pomiary_pol$tmax_9, paired = TRUE, alternative = "less")14.2 Testowanie istotności różnic wariancji
- Pozwala na porównywanie wariancji w dwóch grupach pomiarów
- Zakłada rozkład normalny w obu grupach
- Test ten może być jednostronny lub dwustronny
- Dla wielu wariancji używany jest test Levene’a
pomiary_pol = read.csv("data/pomiary_pol.csv")
pomiary_pol2 = subset(pomiary_pol,
prowincja %in%
c("Niż Wschodniobałtycko-Białoruski",
"Wyżyny Polskie"))var.test(annual_tavg ~ prowincja, data = pomiary_pol2)
F test to compare two variances
data: annual_tavg by prowincja
F = 0.8629, num df = 161, denom df = 178, p-value = 0.3405
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.6384037 1.1690499
sample estimates:
ratio of variances
0.8628984 Interpretacja:
- Wartość p-value dla testu F p = 0.3405 jest większa od założonego poziomu istotności (0.05). Nie ma istotnych różnic między wariancją dla obu grup (Niżu oraz Wyżyn).
14.2.1 Test Levene’a
- Porównywane grupy w testach parametrycznych powinny mieć podobne wariancje
- Do weryfikacji czy zachowana jest homogoniczność wariancji w grupach stosuje się, między innymi, test Levene”a
- \(H_0\) - wariancje są takie same
- \(H_A\) - wariancje się różnią
pomiary_pol = read.csv("data/pomiary_pol.csv")
pomiary_pol2 = subset(pomiary_pol,
prowincja %in%
c("Niż Wschodniobałtycko-Białoruski",
"Wyżyny Polskie"))library(car)
leveneTest(annual_tavg ~ prowincja, data = pomiary_pol2)Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 1.2277 0.2686
339